Эллипса и окружность. Эксцентриситет эллипса.

Теорема 1. Любой эллипс, отличный от окружности может быть получен в результате сжатия окружности к диаметру.

Уравнения

(4)

являются параметрическими уравнениями эллипса.

Определение 2. Эксцентриситетом e эллипса называется число, равное отношению его фокального расстоянию с к длине его большей полуоси a: .

Из определения эллипса следует, что 0 £ e < 1. Для окружности эксцентриситет равен нулю.

Так как 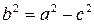, то . Из этого соотношения получаем, что чем ближе e к 1, тем меньше отношение b / a, при одинаковых значениях a тем более продолговатый эллипс.

1. Гипербола. Каноническое уравнение гиперболы

Определение 1. Гиперболой называется множество всех точек плоскости, для каждой из которых модуль разности расстояний до двух данных точек F ₁ и F ₂ той же плоскости есть величина постоянная, меньшая, чем расстояние между точками F ₁, F ₂.

Точки называются фокусами, расстояние | F ₁ F ₂| называется фокальным расстоянием. Обозначаем его через 2 с. Через 2 а обозначим модуль разности от любой точки гиперболы до фокусов. По определению a < c.

| MF ₁| - | MF ₂| = ±2 c. (1)

Находим

| MF ₁| = , | MF ₂| = .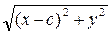

Отсюда получим уравнение гиперболы

. (2)

Обозначаем

и найденное выше уравнение запишем в виде

. (3)

Уравнение (3) называется каноническим уравнением гиперболы. Отрезки | MF ₁|, | MF ₂| называются фокальными радиусами точки M.

Дата добавления: 2015-07-11