Исследование формы эллипса.

1⁰. Координатные оси являются осями симметрии эллипса. Начало координат - центр симметрии.

Так как координаты в каноническом уравнении эллипса имеют четную степень, то если 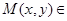эллипсу, то и , 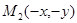- принадлежат эллипсу.

2⁰. С координатными осями эллипса пересекается в точках , , , , так как эти точки удовлетворяют уравнению. Они называются вершинами эллипса.

3⁰. Координаты любой точки удовлетворяют условиям:

,

то есть эллипс лежит внутри прямоугольника со сторонами и .

4⁰. Рассмотрим эллипс в первой четверти, где .

.

Очевидно, что если эллипс имеет вид:

- большая ось.

- малая ось.

- большая полуось.

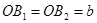- малая полуось.

- фокусное расстояние.

- центр.

При 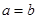- окружность, есть частный случай эллипса.

Дата добавления: 2015-07-11