Типы кривых второго порядка.

Гл. 4. Кривые второго порядка.

Типы кривых второго порядка.

Определение: Множество точек плоскости координаты которых, в некоторой декартовой системе координат , удовлетворяют уравнению:

, называется алгебраической кривой второго порядка.

Причем, хотя бы один из коэффициентов отличен от 0.

К кривым второго порядка относятся эллипс, частичным случаем которого является окружность, гипербола и парабола.

Эти кривые получаются, если прямой круговой конус (конус вращения) пересечен плоскостями не проходящими через вершину конуса. Поэтому, эти кривые называют коническими сечениями.

Кроме того, уравнение второго порядка относительно и может определять:

- пара пересекающихся прямых с уравнением .

- пару параллельных прямых с уравнением .

- одну прямую (или ).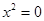

- одну точку -

- пустое множество точек или мнимое геометрическое место .(или , ).

Дата добавления: 2015-07-11