Определение, уравнение, график.

Определение: Гипербола - это множество точек плоскости, абсолютная величина разности расстояний от каждой из который, до двух данный точек, называемых фокусами гиперболы, есть величина постоянная равная .(меньшая, чем расстояния между фокусами ) .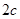

,

^{каноническое уравнение гиперболы.}

где или .

Исследование формулы:

1⁰. По записи уравнения очевидно, что кривая симметрична относительно осей и , а так же начала координат.

2⁰. Гипербола пересекает в точке и , и не пересекает .

3⁰. Координаты любой точки удовлетворяют условиям:

, так как .

Таким образом гипербола расположена вне полосы именуемой симметричной относительно .

4⁰. В первой четверти, где 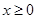и 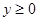, если возрастает, то так же возрастает.

На основании этих свойств гипербола имеет вид:

- действительная ось .

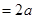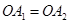- действительная полуось.

- мнимая ось .

- мнимая полуось.

- фокусное расстояние .

- центр гиперболы.

Точки и - вершины гиперболы.

По .

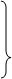
(**) сопряженные гиперболы.

Для (**) - мнимая ось, - действительная.

Дата добавления: 2015-07-11