Парабола. Определение: Параболой называется множество точек плоскости

Определение: Параболой называется множество точек плоскости, каждая из которых находиться на одинаковом расстоянии от данной точки, называемой фокусом параболы и данной прямой называемой директрисой.

Обозначим расстояние от фокуса до директрисы за . - произвольная точка параболы.

- уравнение параболы.

.

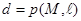
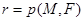По .

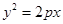- каноническое уравнение.

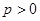
- параметр параболы.

- фокальный радиус точки .

Исследование формулы:

1⁰. Из уравнения 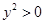, , 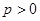, значит 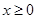. Таким образом, парабола лежит в правой полуплоскости.

2⁰. Проходит через начало координат.

3⁰. При возрастании , так же возрастает.

Таким образом, парабола имеет вид:

График параболы вытянут вдоль той оси, чья координата в первой степени в ее уравнении.

Если парабола задана: , то

Уравнение - есть уравнение параболы симметричной относительно прямой параллельной оси ординат и вершиной в точке координатами .

Выделяем полный квадрат:

.

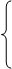Используем параллельный перенос:

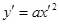
, Пусть .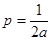

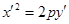Пример: 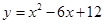. Построить параболу.

Дата добавления: 2015-07-11