Парабола. Параболой называется геометрическое место точек на плоскости

Параболой называется геометрическое место точек на плоскости, равноудаленных от фиксированной точки (фокуса) и данной прямой, не проходящей через эту точку (директрисы), лежащих на этой же плоскости.

Существуют 4 вида канонических уравнений параболы:

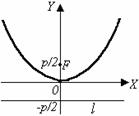
	х^2= 2ру. Фокус F(0; 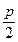), уравнение директрисы: у = – .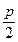
	х^2= –2ру. Фокус F(0; – 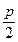), уравнение директрисы: у = .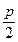
	у^2= 2рх. Фокус F(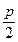; 0), уравнение директрисы: х = – .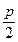
	у^2=–2рх. Фокус F(– 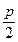; 0), уравнение директрисы: х = .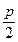

Термины и обозначения основных элементов параболы: O – вершина параболы; F – фокус параболы; p – параметр параболы (расстояние от фокуса F до директрисы).

Эксцентриситет параболы равен единице: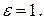

Если вершина параболы находится в точке , а ее директриса лежит на прямой, параллельной оси Ох, то ее уравнение имеет вид:

или .

Если вершина параболы находится в точке , а ее директриса лежит на прямой, параллельной оси Оу, то ее уравнение имеет вид:

или .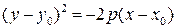

----------------------------------------------------------------------------------------------------------------

Кривые второго порядка. Стр. 3

Дата добавления: 2015-07-11