Парабола.

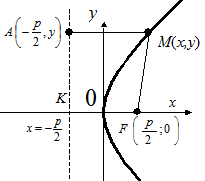Параболою називається геометричне місце точок, для кожної з яких відстань до деякої фіксованої точки площини, яку називають фокусом, дорівнює відстані до деякої фіксованої прямої, званої директрисою.

Фокус параболи позначається буквою F, відстань від фокуса до директриси - буквою p. Число p називається параметром параболи

Візьмемо довільну точку параболи M (x, y). Позначимо FM = r, d - відстань до директриси

Канонічне рівняння параболи

y²=2p (4.8)

Парабола - лінія другого порядку. Вона симетрична відносно осі ОХ.

Директриса даної параболи має рівняння

(4.9)

Фокальний радіус довільної точки M (x, y) параболи може бути обчислений за формулою 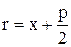(4.10)

Парабола, рівняння якої 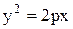виглядає наступним чином.

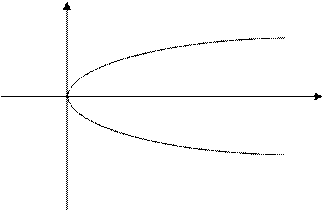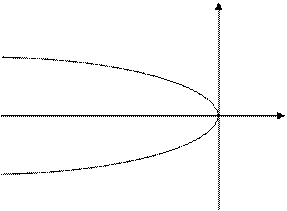Аналогічно y²=-2px

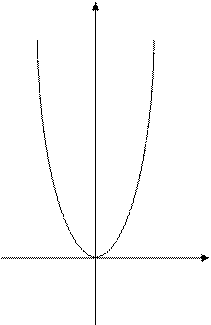x²=2px

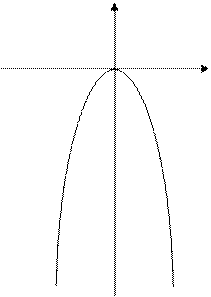
x²=-2px

Приклад. Скласти рівняння параболи, вершина якої знаходиться на початку координат, знаючи, що: парабола розташована в правій півплощині симетрично щодо осі ОХ і її параметр p = 3.

Розв’язок. Якщо парабола розташована в правій півплощині, то її канонічне рівняння

y²=2px, або y²=6x.

(За умовою p=3, 2p=6).

Приклад. Знайти фокус F і рівняння директриси параболи y²=24x.

Розв’язок. З рівняння параболи випливає, що p=12. А значить у фокуса параболи координати F(6;0).

Директриса параболи визначається за (4.9) рівнянням 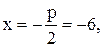тобто x+6=0.

Завдання для самоконтролю.

1. Скласти рівняння параболи, вершина якої знаходиться на початку координат, знаючи, що:

1) парабола розташована в лівій півплощині симетрично щодо осі ОХ, і її параметр p = 0,5;

2) парабола розташована у верхній півплощині симетрично щодо осі OY, і її параметр p = 1/4;

3) парабола розташована в нижній півплощині симетрично щодо осі OY, і її параметр p = 3.

Відповідь: y²= -x; x²=1/2y; x²=-6y.

2. Обчислити фокальний радіус точки М параболи y²=20x, якщо абсциса точки М дорівнює 7.

Відповідь: 12.

МОДУЛЬ 2. ОСНОВИ ДИФЕРЕНЦІАЛЬНОГО ЧИСЛЕННЯ

Тема 5. Границі функції

Функція

Якщо кожному значенню змінної x, що належить деякій області, відповідає одне певне значення іншої змінної у, то у називається функцією змінної х. Символічно записуватимемо y=f(x). При цьому змінна x називається незалежною змінною або аргументом.

Запис y=C, де С – постійна, позначає функцію, значення якої при будь-якому значенні x одне й те ж та дорівнює С.

Безліч значень x, для яких можна визначити значення функції у за правилом f(x), називається областю визначення функції.

Помітимо, що числова послідовність також є функцією, область визначення якої співпадає з безліччю натуральних чисел.

До основних елементарних функцій відносяться всі функції, що вивчаються в шкільному курсі математики:

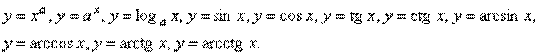
Поняття границі числової послідовності

Почнемо з поняття границі числової послідовності.

Число а називається границею послідовності x = { x_n}, якщо для довільного наперед заданого скільки завгодно малого позитивного числа e знайдеться таке натуральне число N, що при всіх n>N виконується нерівність |x_{n_}- a| <e.

Якщо послідовність має границю (кінцеву або нескінченну), то говорять, що вона сходиться, інакше говорять, що вона розходиться.

Границя функції

Нехай функція y=f(x) визначена в деякому околі точки а. Припустимо, що незалежна змінна x необмежено наближається до числа а. Це означає, що ми можемо надавати х значення скільки завгодно близькі до а, але не рівні а. Позначатимемо це так x → а. Для таких x знайдемо відповідні значення функції. Може трапитися, що значення f(x) також необмежено наближаються до деякого числа b. Тоді говорять, що число b є границя функції f(x) при x → а.

Якщо нерівність | f(x)-b|< ε виконується тільки в лівому (правому) напівоколі точки а, то число b називається границею функції f(x) при x → а зліва (справа) або лівобічною (правобічною) межею і позначається:

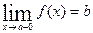або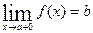

Помітимо, що якщо границя зліва й справа в точці а для функції f(x) не співпадають, то функція не має границі (двостороннього) в точці а.

Приклади.

Розглянемо функцію y=f(x), визначену на відрізку [0,1] таким чином

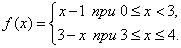
Знайдемо границі функції f(x) при x → 3. Очевидно, що

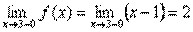, а .

.

.

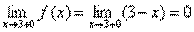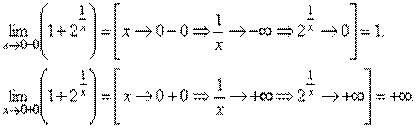
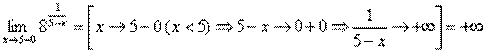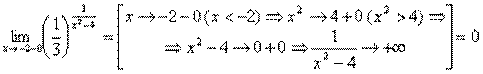Нескінченно великі функції

Функція f(x) називається нескінченно великою при x → a, якщо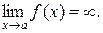

Приклади.

.

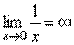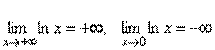
Нескінченно малі функції і їх основні властивості

Функція y=f(x) називається нескінченно малою при x → a або при x → ∞, якщо або 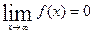, тобто нескінченно мала функція – це функція, границя якої в даній точні дорівнює нулю.

Приклади.

Функція f(x)=(x-1)^2 є нескінченно малою при x →1, тому що 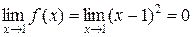(див. рис.). Функція f(x)= tgx – нескінченно мала при x®0. f(x)= ln (1+x) – нескінченно мала при x®0. f(x)= 1/x– нескінченно мала при x ®. ¥

Встановимо наступне важливе співвідношення:

Теорема. Якщо функцію y = f(x) можна представити при x → a у вигляді суми постійного числа b й нескінченно малої величини α(x): f (x)=b+α(x) тоді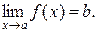

Навпаки, якщо 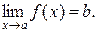то f (x)=b+α(x), де а(x) – нескінченно мала при x®a.

Розглянемо основні властивості нескінченно малих функцій.

Теорема 1. Алгебраїчна сума двох, трьох і взагалі будь-якого кінцевого числа нескінченно малих є функція нескінченно мала.

Теорема 2. Добуток нескінченно малої функції а(x) на обмежену функцію f(x) при x®a (або при x →∞ ) є нескінченно мала функція.

З теореми витікають:

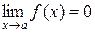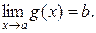Наслідок 1. Якщо й , то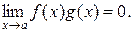

Наслідок 2. Якщо 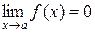й c =const, то .

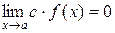Теорема 3. Відношення нескінченно малої функції α(x) до функції f(x), границя якої відмінна від нуля, є нескінченно мала функція.

Співвідношення між нескінченно малими

і нескінченно великими функціями

Теорема 1. Якщо функція f(x) є нескінченно великою при x®a, то функція 1/ f(x) є нескінченно малою при x®a.

Приклади.

1. Ясно, що при x →+∞ функція y=x²+1 є нескінченно великою. Але тоді згідно сформульованій вище теоремі функція 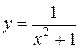– нескінченно мала при x →+∞, тобто .

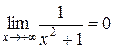2. .

.

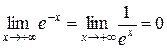Теорема 2. Якщо функція f(x) - нескінченно мала при x®a (або x →∞ ) і не обертається в нуль, то y=1/f(x) є нескінченно великою функцією.

Приклади.

.

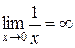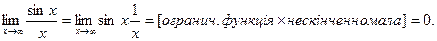
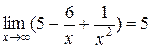, оскільки функці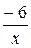ї і 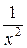- нескінченно малі при x →+∞, тоді 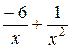, як сума нескінченно малих функцій є функція нескінченно мала. Функція ж 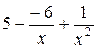є сумою постійного числа й нескінченно малої функції. Отже, згідно теореми 1 для нескінченно малих функцій одержуємо потрібну рівність.

Таким чином, прості властивості нескінченно малих і нескінченно великих функцій можна записати за допомогою наступних умовних співвідношень (при А≠0):

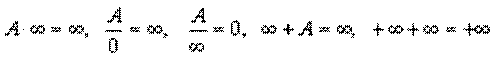Теореми про границі

Теорема 1. Границя алгебраїчної суми двох, трьох і взагалі будь-якого числа функцій дорівнює алгебраїчній сумі меж цих функцій, тобто

.

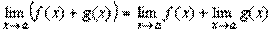Приклад.

.

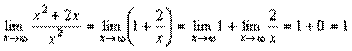Теорема 2. Границя добутку двох, трьох і взагалі кінцевого числа функцій дорівнює добутку границь цих функцій:

.

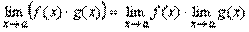Наслідок 1. Постійний множник можна виносити за знак границі:

.

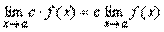Наслідок 2. Границя ступеня рівна ступеню границі:

.

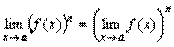Приклад.

.

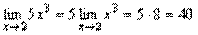Теорема 3. Границя відношення двох функцій дорівнює відношенню границь цих функцій, якщо границя знаменника відмінна від нуля, тобто

.

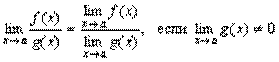Приклади.

1.

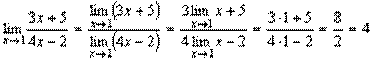
2. .

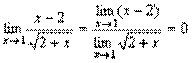Розглянемо 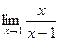. При x® 1 чисельник дробу прагне до 1, а знаменник прагне до 0. Але, оскільки 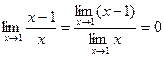, тобто 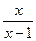є нескінченно мала функція при x® 1, то .

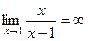Типи невизначеності і способи їх розкриття

Часто при обчисленні границі будь-якої функції, безпосереднє застосування теорем про границі не приводить до бажаної мети. Так, наприклад, не можна застосовувати теорему про границю дробу, якщо її знаменник прагне до нуля. Тому часто перш, ніж застосовувати ці теореми, необхідно тотожно перетворити функцію, границю якої ми шукаємо.

Умовні вирази

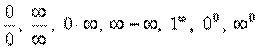
характеризують типи невизначеності і застосовуються для позначення змінних величин, при обчисленні границі яких не можна відразу застосовувати загальні властивості границь.

Розглянемо деякі прийоми розкриття невизначеностей.

.

.

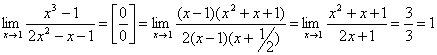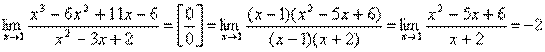При розкладанні чисельника на множники скористалися правилом поділення полінома на поліном “кутом”. Оскільки число x=1 є коренем полінома

x³–6x² +11x– 6, то при діленні одержимо

.

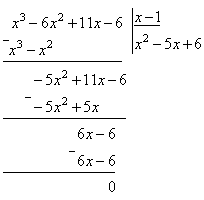
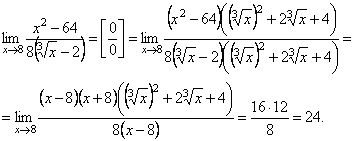
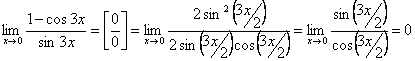II. Невизначеність .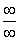

.

При обчисленні границі чисельник і знаменник даного дробу розділили на x в старшому ступені.

.

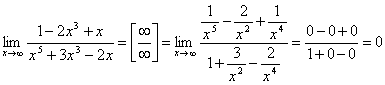
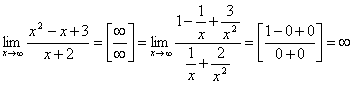
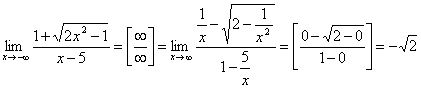При обчисленні границі скористалися рівністю 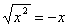, якщо x<0.

Види невизначеностей з допомогою алгебраїчних перетворень функції, що стоїть під знаком границі, приводять до одного з розглянутих вище випадків або .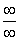

III. Невизначеність 0·∞.

.

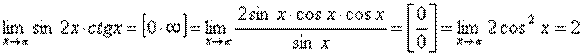IV. Невизначеність ∞ –∞.

1.

2.

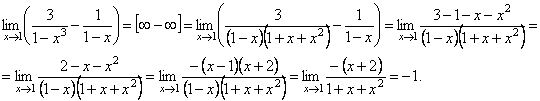
3. .

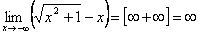Дата добавления: 2015-07-12