Приклади.

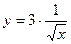Якщо , то

y = x ³ – 3 x ² + 5 x + 2. Знайдемо y '(–1).

y ' = 3 x ² – 6 x + 5. Отже, y '(–1) = 14.

y = ln x · cos x, то y ' = (ln x) ' cos x + ln x (cos x) ' =1/ x ∙cos x – ln x · sin x.

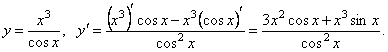
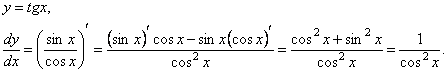
Таким чином,

Аналогічно для y= ctgx,

Завдання до самоконтролю.

	y=3x^2+2x-6
	y=2x^3(8x+11)
	y =3+2 x sin x
	y=(x^2+1) arctg x

Похідна складної функції

Нехай у = f(u), а u= u(x). Одержуємо функцію у, залежну від аргументу x:
у = f(u(x)). Остання функція називається функцією від функції або складною функцією.

Областю визначення функції у = f(u(x)) є або вся область визначення функції u=u(x) або та її частина, в якій визначаються значення u, що не виходять з області визначення функції y= f(u).

Операція "функція від функції" може проводитися не один раз, а будь-яке число разів.

Встановимо правило диференціювання складної функції.

Теорема. Якщо функція u = u(x) має в деякій крапці x₀ похідну 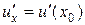і приймає в цій точці значення u₀ = u (x₀), а функція y= f(u) має в точці u₀ похідну у'_u = f '(u₀), то складна функція у = f(u(x)) у вказаній точці x₀ теж має похідну, яка дорівнює у' _x = f '(u₀)· u '(x₀), де замість u повинен бути підставлений вираз u= u(x).

Таким чином, похідна складної функції дорівнює добутку похідної даної функції по проміжному аргументу u на похідну проміжного аргументу по x.

Приклади.

1) у = sin x². Тоді .

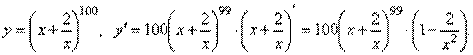
2)

3)

4)

Похідна оберненої функції

Теорема. Якщо для функції y=f(x) існує обернена функція x=g(y), яка в деякій точці у₀ має похідну g '(v₀), відмінну від нуля, то у відповідній точці x₀=g (x₀) функція y=f(x) має похідну f '(x₀), яка дорівнює , тобто справедлива формула

Цю формулу можна записати у вигляді .

Приклади:

Логарифмічне диференціювання

Диференціювання багатьох функцій спрощується, якщо їх заздалегідь прологарифмувати. Для цього поступають таким чином. Якщо потрібно знайти у' з рівняння y=f(x), то можна:

1) Прологарифмувати обидві частини рівняння

ln y = ln f(x) =

2) Продиференціювати обидві частини рівності, вважаючи ln у складною функцією від змінної x:

3) Виразити y ' = y · = f(x) ·(ln f(x))'.

Приклади.

1) у = х^а – степенева функція з довільним показником.

.

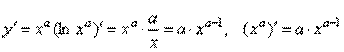2)

Показово-степенева функція і її диференціювання

Показово-степеневою функцією називається функція вигляду у = u^v, де u=u(x), v=v(x).

Логарифмічне диференціювання застосовується для знаходження похідної від показово-степеневої функції.

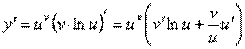
Приклади.

.

Таблиця похідних

Об'єднаємо в одну таблицю всі основні формули і правила диференціювання, виведені раніше. Усюди вважатимемо u=u(x), v=v(x), С =const. Для похідних основних елементарних функцій користуватимемося теоремою про похідну складної функції.

Правила диференціювання

1)

2)

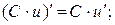
3)

4)

5)

Таблиця похідних

1.
2.
3.
4.
5.
6.
7.
8.
9.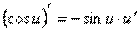
10.
11.
12.
13.
14.
15.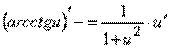
16.

Приклади.

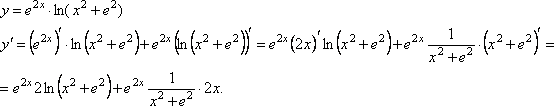
Знайти у' (–1).

Похідні вищих порядків

Похідна від першої похідної називається похідною другого порядку або другою похідною від даної функції y=f(x) і позначається y'' або f''(x). Отже, y''=(у')'.

Наприклад, якщо у = х⁵, то y'= 5x⁴, а y''= 20 x ³.

Аналогічно, у свою чергу, похідну другого порядку теж можна диференціювати. Похідна від другої похідної називається похідною третього порядку або третьою похідною і позначається y''' або f'''(x).

Взагалі, похідною n-го порядку від функції f(x) називається похідна (перша) від похідної (n – 1) -го порядку і позначається символом у⁽ⁿ⁾ або f⁽ⁿ⁾(x): у⁽ⁿ⁾ = (у ^(n-1))'.

Таким чином, для знаходження похідної вищого порядку від даної функції послідовно знаходять все її похідні нижчих порядків.

Приклади.

1) Знайти похідну четвертого порядку функції y= ln x.

.

2) Знайти похідну другого порядку від функції

.

2) Знайти похідну n-го порядку функції у = e^kx.

y'= k·e^kx, y''= k²·e^kx, y''' = k³·e^kx, …, y⁽ⁿ⁾= k ⁿ·e^kx.

3) Знайти похідну n-го порядку функції у = sin x.

Маємо

Дата добавления: 2015-07-12