
|
Читайте также: |
1) Знайти найбільше і якнайменше значення функції  на відрізку [–2; –0,5].
на відрізку [–2; –0,5].
Знайдемо критичні точки функції. 
Обчислимо значення функції в знайденій крапці і на кінцях заданого відрізка.
 Отже,
Отже,

2) Знайти найбільше і якнайменше значення функції y=x-2 -·ln x на [1; e ].

Опуклість і угнутість графіка функції. точки перегину
 Графік функції y=f(x) називається опуклим на інтервалі (а; b), якщо він розташований нижче будь-якою своєї дотичної на цьому інтервалі.
Графік функції y=f(x) називається опуклим на інтервалі (а; b), якщо він розташований нижче будь-якою своєї дотичної на цьому інтервалі.
Графік функції y=f(x) називається увігнутим на інтервалі (а; b), якщо він розташований вище будь-якою своєї дотичної на цьому інтервалі.
На рисунку показана крива, опукла на
(а; b) і увігнута на (b; с).
 Приклади.
Приклади.
Півколо  є опуклим на [–1; 1].
є опуклим на [–1; 1].
Парабола у = x2 увігнута на інтервалі (- 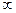 ; +
; + 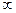 ).
).
Графік функції в одних інтервалах може бути опуклим, а в інших увігнутим. Так графік функції у =sin x на [0;2 π ], опуклий в інтервалі (0; π) і увігнутий в (π; 2 π).
Розглянемо достатню ознаку, що дозволяє встановити, чи буде графік функції в даному інтервалі опуклим або увігнутим.
Теорема. Нехай y=f(x) є диференційованою на (а; b). Якщо в усіх точках інтервалу (а; b) друга похідна функції у=f(x) від’ємна, тобто f''(x)< 0, то графік функції на цьому інтервалі опуклий, якщо f''(x)> 0 – увігнутий.
Приклади.
 1) Встановити інтервали опуклості і угнутості кривої
1) Встановити інтервали опуклості і угнутості кривої  у = 2 – x2.
у = 2 – x2.
Знайдемо у '' і визначимо, де друга похідна додатна і де від’ємна. у' = –2x, y'' = –2 < 0 на (–∞; +∞), отже, функція усюди опукла.
2) у = ex. Оскільки y'' = ex > 0 при будь-яких x, то крива усюди увігнута.
 3) у = x3. Оскільки y'' = 6x, то y'' < 0 при x < 0 і y'' > 0 при x > 0. Отже, при x < 0 крива опукла, а при x > 0 увігнута.
3) у = x3. Оскільки y'' = 6x, то y'' < 0 при x < 0 і y'' > 0 при x > 0. Отже, при x < 0 крива опукла, а при x > 0 увігнута.
Точка графіку безперервної функції, що відділяє його опуклу частину від увігнутої, називається точкою перегину.
 Очевидно, що в точці перегину дотична, якщо вона існує, перетинає криву, оскільки з одного боку від цієї точки крива лежить під дотичною, а з другого боку – над нею.
Очевидно, що в точці перегину дотична, якщо вона існує, перетинає криву, оскільки з одного боку від цієї точки крива лежить під дотичною, а з другого боку – над нею.
Визначимо достатні умови того, що дана точка кривої є точкою перегину.
Теорема. Нехай крива визначається рівнянням у = f(x). Якщо f ''(x0)= 0 або f ''(x0) не існує і під час переходу через значення x = x0 похідна f ''(x) змінює знак, то точка графіка функції з абсцисою x = x0 є точка перегину.

Приклади. Знайти точки перегину і визначити інтервали опуклості і угнутості кривих.
1) 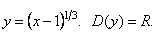
Знайдемо похідні заданої функції першого та другого порядку.

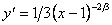 .
.
 .
.
Друга похідна не існує при x = 1. Дослідимо цю точку на можливий перегин.
Отже, точка перегину x = 1. Функція опукла на (1; + 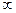 ), увігнута на (–
), увігнута на (– 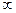 ; 1).
; 1).
2)


Можливі точки перегину знайдемо, вирішивши рівняння 2x2 – 1 = 0. Звідси 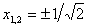 .
.
Точки перегину 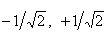 . Функція опукла на
. Функція опукла на  і увігнута на
і увігнута на  .
.
3) у = ln (1 – x2). Область визначення функції D(y)= (-1; 1).
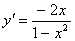 .
.

при всіх x з (–1; 1). Отже, f(x) опукла на (–1; 1).
Асимптоти графіка функції
Пряма називається асимптотою графіка функції у = f(x), якщо відстань від змінної точки M графіка до цієї прямої при видаленні точки M в нескінченність прагне до нуля, тобто точка графіка функції при своєму прагненні в нескінченність повинна необмежено наближатися до асимптоти.
Надалі розрізнятимемо асимптоти вертикальні й похилі.
Для відшукання вертикальних асимптот графіка функції у = f(x) потрібно знайти ті значення x = x0, при яких функція звертається в нескінченність (терпить нескінченний розрив). Тоді вертикальна асимптота має рівняння x = x0.
Приклад.
Знайти вертикальні асимптоти графіка функції  .
.
Оскільки  , то пряма x =2 є вертикальною асимптотою.
, то пряма x =2 є вертикальною асимптотою.
 .
.
Пряма x = 0 – вертикальна асимптота.
Оскільки асимптота – це пряма, то якщо крива у = f(x) має похилу асимптоту, те її рівняння буде у = kx + b. Наша задача знайти коефіцієнти k і b.
Теорема. Пряма у = kx + b служить похилою асимптотою при x → +∞ для графіка функції у = f(x) тоді і тільки тоді, коли 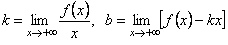 .
.
Аналогічне твердження вірне і при x → –∞.
Приклади. Знайти асимптоти кривих.
1) 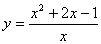 .
.
Вертикальні:
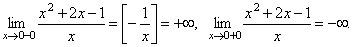
x = 0 – вертикальна асимптота.
Похилі:
 .
.
При x → -∞ набудемо ті ж значень k і b. Отже, пряма у = x + 2 є похилою асимптотою.
2) у = e–x sin x + x.
Функція визначена і безперервна на всій числовій прямій, отже, вертикальних асимптот немає.
а)  .
.
Отже, при x → +∞ похила асимптота у= х.
б) 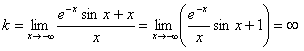 , оскільки
, оскільки
 , тому при x → - ∞ похилих асимптот немає.
, тому при x → - ∞ похилих асимптот немає.
3) у = x – 2arctg x.
Вертикальних асимптот немає.
а)  .
.
 . Похила асимптота у = x – π при
. Похила асимптота у = x – π при 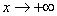 .
.
б)  при
при  .
.
Загальна схема дослідження функції і побудови графіків
1. Знайти область допустимих значень (ОДЗ) і точки розриву функції.
2. Знайти точки перетину графіка функції з осями координат.
3. Провести дослідження функції за допомогою першої похідної, тобто знайти точки екстремуму функції і інтервали зростання і спадання.
4. Дослідити функцію за допомогою похідної другого порядку, тобто знайти точки перегину графіка функції і інтервали його опуклості і угнутості.
5. Знайти асимптоти графіка функції: а) вертикальні, b) похилі.
6. На підставі проведеного дослідження побудувати графік функції.
Перед побудовою графіка корисно встановити, чи не є дана функція парною або непарною. (функція називається парною, якщо при зміні знаку аргументу значення функції не міняється: f(-х) = f(x) і функція називається непарною, якщо f(-х) = -f(x)). В цьому випадку достатньо дослідити функцію і побудувати її графік при додатних значеннях аргументу, що належать ОДЗ. При від’ємних значеннях аргументу графік добудовується на тій підставі, що для парної функції він симетричний щодо осі Oy, а для непарної – щодо початку координат.
Приклади. Дослідити функції і побудувати їх графіки.
1) 
 .
.
1. Область визначення функції D(у)= (– 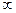 ; +
; + 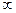 ). Точок розриву немає.
). Точок розриву немає.
Перетин з віссю Ох: x = 0,у=0.
Функція непарна, отже, можна досліджувати її тільки на проміжку [0, + 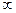 ).
).
2.  . Критичні точки: x1 = 1; x2= –1.
. Критичні точки: x1 = 1; x2= –1.


3. 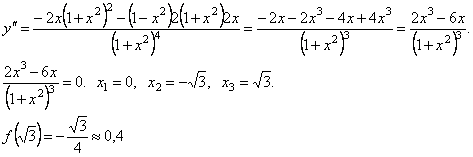
4.  а) Вертикальних асимптот немає
а) Вертикальних асимптот немає
б) 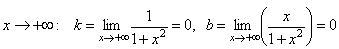 . Асимптота – у = 0.
. Асимптота – у = 0.


Дата добавления: 2015-07-12; просмотров: 162 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Приклади. | | | Завдання до самоконтролю |