Метод Гауса

Раніше розглянуті методи можна застосовувати при рішенні тільки тих систем, в яких число рівнянь співпадає з числом невідомих, причому визначник системи повинен бути відмінний від нуля. Метод Гауса є більш універсальним і придатний для систем з будь-яким числом рівнянь. Він полягає в послідовному виключенні невідомих з рівнянь системи.

Знову розглянемо систему з трьох рівнянь з трьома невідомими:

.

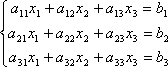Перше рівняння залишимо без зміни, а з 2-го і 3-го виключимо складові, що містять x₁. Для цього друге рівняння розділимо на а₂₁ і помножимо на –а₁₁, а потім складемо з 1-им рівнянням. Аналогічно третє рівняння розділимо на а₃₁ і помножимо на –а₁₁, а потім складемо з першим. В результаті початкова система прийме вигляд:

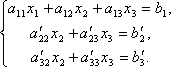
Тепер з останнього рівняння виключимо складову, що містить x₂. Для цього третє рівняння розділимо на а'₃₂, помножимо на -а'₂₂ і складемо з другим. Тоді матимемо систему рівнянь:

Звідси з останнього рівняння легко знайти x₃, потім з 2-го рівняння x₂ і, нарешті, з 1-го – x₁.

При використовуванні методу Гауса рівняння при необхідності можна міняти місцями.

Часто замість того, щоб писати нову систему рівнянь, обмежуються тим, що виписують розширену матрицю системи:

,

потім приводять її до трикутного або діагонального вигляду за допомогою елементарних перетворень.

До елементарних перетворень матриці відносяться наступні перетворення:

- перестановка рядків або стовпців;

- множення рядка на число, відмінне від нуля;

- додавання до одного рядка інших рядків.

Приклади:

1. Вирішити систему рівнянь методом Гауса.

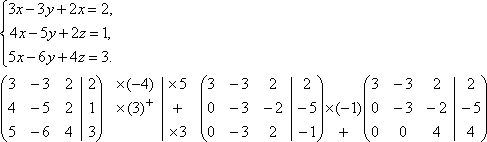
Повернувшись до системи рівнянь, матимемо

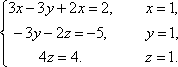
2. Вирішити систему рівнянь

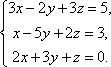
Випишемо розширену матрицю системи і зведемо її до трикутного вигляду.

Розділимо другий рядок матриці на 2 і поміняємо місцями перший і третій стовпчики. Тоді перший стовпець відповідатиме коефіцієнтам при невідомій z, а третій – при x.

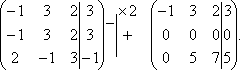
Повернемося до системи рівнянь.

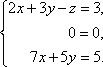
З третього рівняння виразимо одну невідому через іншу і підставимо в перше

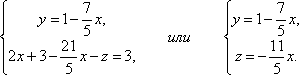
Таким чином, система має нескінченну безліч рішень.

Дата добавления: 2015-07-12