Приклади. Прологарифмуємо цю рівність

.

.

.

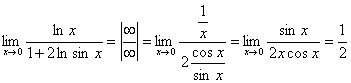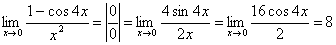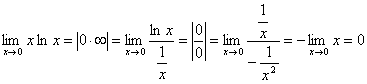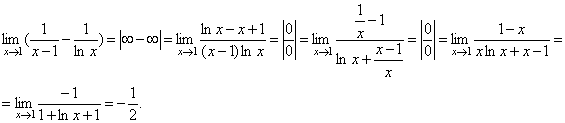
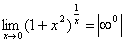
Позначимо .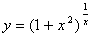

Прологарифмуємо цю рівність 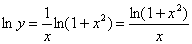. Знайдемо .

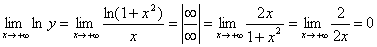Оскільки ln y функція безперервна, то 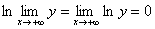. Отже, 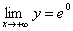або .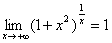

Застосування похідних до дослідження функцій і побудови графіків

Теорема 1. (Необхідна і достатня умови зростання функції)

Якщо функція y=f(x), що диференціюється, зростає на [ а, b ], то її похідна невід’ємна на цьому відрізку, f '(x) ≥ 0.

Обернено. Якщо функція y=f(x) безперервна на [ а, b ], є диференцюємою на (а, b) і її похідна додатна на цьому відрізку, f ' (x) ≥ 0 для a<x<b, то f(x) зростає на [ а, b ].

Теорема 2. Якщо f(x) спадає на [ а,b ], то 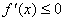на цьому відрізку. Якщо 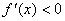на (а; b), то f(x) спадає на [ а, b ], в припущенні, що f(x) безперервна на [ а, b ].

Приклад. Визначити інтервали монотонності функції .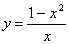

Розв’язання.

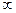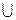Область визначення заданої функції D(y) = (- ; 0) (0; + ).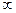

.

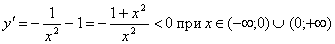Отже, f(x) – спадає на (- 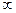; 0) і (0; + ).

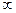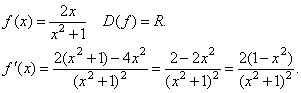
Знайдемо проміжки, на яких похідна заданої функції додатна або від’ємна методом інтервалів.

Отже, f(x) – спадає на (– 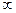; –1] і [1; + 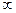), зростає на відрізку [–1; 1].

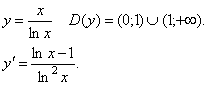
Використовуючи метод інтервалів, одержимо f(x) спадає на (0; 1) і (1; e ], зростає на [ e; + ).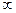

Екстремуми функції

Функція y=f(x) в точці x₀ має максимум, якщо значення функції в цій точці більше, ніж її значення в усіх точках деякого інтервалу, що містить точку x_0, тобто якщо існує така околиця точки x_0, що для всіх x ≠ x _0, що належать цій околиці, має місце нерівність f(x) < f(x ₀ ).

Функція y=f(x) має мінімум в точці x₀, якщо існує така околиця точки x₀, що для всіх x ≠ x ₀, що належать цій околиці, має місце нерівність f(x) > f(x₀).

Точки, в яких функція досягає максимуму і мінімуму, називаються точками екстремуму, а значення функції в цих точках - екстремумами функції.

Звернемо увагу на те, що функція, визначена на відрізку, може досягати максимуму і мінімуму тільки в точках, укладених усередині даного відрізка.

Відмітимо, що якщо функція має в крапці максимум, то це не означає, що в цій крапці функція має найбільше значення у всій області визначення. З визначення максимуму виходить тільки, що це найбільше значення функції в точках, достатньо близьких до точки максимуму.

Теорема 1. (Необхідна умова існування екстремуму.) Якщо функція y=f(x), що диференціюється, має в крапці x= x₀ екстремум, то її похідна в цій крапці звертається в нуль.

Теорема 2. (Достатня умова існування екстремуму.) Нехай функція безперервна на деякому інтервалі, що містить критичну точку x₀, і є диференційованою в усіх точках цього інтервалу (окрім, мабуть, самої точки x₀). Якщо при переході зліва направо через цю крапку похідна міняє знак з плюса на мінус, то в точці x = x₀ функція має максимум. Якщо ж під час переходу через x₀ зліва направо похідна міняє знак з мінуса на плюс, то функція має в цій крапці мінімум.

Таким чином, якщо

f '(x) >0 при x<x₀ і f '(x)< 0 при x> x₀, то x₀ – точка максимуму;

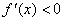при x<x₀ і f '(x)> 0 при x> x₀, то x₀ – точка мінімуму.

Правило дослідження функції y=f(x) на екстремум:

1. Знайти область визначення функції f(x).

2. Знайти першу похідну функції f '(x).

3. Визначити критичні точки, для цього:

- знайти дійсні корені рівняння f '(x)= 0;

- знайти всі значення x при яких похідна f '(x) не існує.

4. Визначити знак похідної зліва і праворуч від критичної точки. Оскільки знак похідної залишається постійним між двома критичними точками, то достатньо визначити знак похідної в якій-небудь одній крапці зліва і в одній крапці праворуч від критичної точки.

5. Обчислити значення функції в точках екстремуму.

Приклад. Дослідити функції на мінімум і максимум функцію .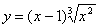

Розв’язання.

Область визначення функції D(y)=R.

Знайдемо похідну заданій функції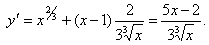

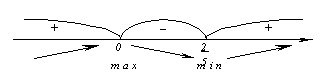
Визначимо критичні точки 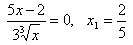. Похідна не існує при х₂= 0. Отже, критичні точки: 0 і 2/5. Нанесемо їх на числову вісь і визначимо знак похідної на кожному з одержаних проміжків.

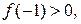
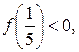
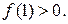Таким чином

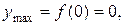
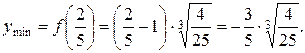
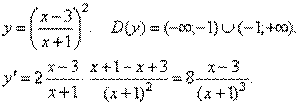
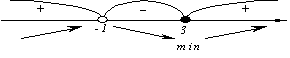
Критична точка функції x =3. Точка x= –1 не входить в область визначення функції.

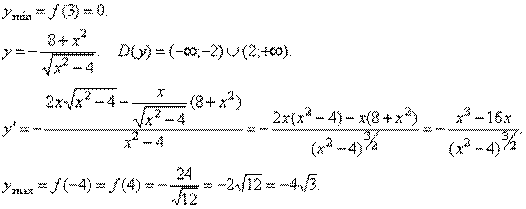
Найбільше й якнайменше значення функції на відрізку

Найбільшим значенням функції на відрізку називається найбільше зі всіх її значень на цьому відрізку, а найменшим – найменше зі всіх її значень.

Правило знаходження найбільшого і якнайменшого значень функції на відрізку[ а, b ]:

1. Знайти всі критичні точки функції в інтервалі (а, b) і обчислити значення функції в цих точках.

2. Обчислити значення функції на кінцях відрізка при x = а, x = b.

3. Зі всіх набутих значень вибрати найбільше і якнайменше.

Дата добавления: 2015-07-12