Приклади. Знайти 2A–B, якщо, .

.

Знайти 2A–B, якщо, .

.

Нехай

. Знайти C= –3A+4B.

Матрицю С знайти не можна, оскільки матриці А і B мають різні розміри.

Множення матриць. Ця операція здійснюється по своєрідному закону. Перш за все, зауважимо, що розміри матриць–співмножників повинні бути узгоджені. Перемножувати можна тільки ті матриці, у яких число стовпців першої матриці співпадає з числом рядків другої матриці (тобто довжина рядка першого дорівнює висоті стовпця другого). Добутком матриці А на матрицю B називається нова матриця C=AB, елементи якої складаються таким чином:

.

Таким чином, наприклад, щоб одержати у добутку (тобто в матриці С) елемент, що стоїть в 1-у рядку і 3-у стовпці c₁₃, потрібно в першій матриці узяти 1-й рядок, у другій – 3-й стовпець, і потім елементи рядка помножити на відповідні елементи стовпця й одержані добутки скласти. І інші елементи матриці-добутку отримують за допомогою аналогічного добутку рядків першої матриці на стовпці другої матриці.

У загальному випадку, якщо ми помножуємо матрицю А = (a_ij) розміром m´n на матрицю B = (b_ij) розміром n´p, то одержимо матрицю С розміру m´p, елементи якої обчислюються таким чином: елемент c_ij виходить в результаті добутку елементів i -го рядка матриці А на відповідні елементи j -го стовпця матриці B і їх додавання.

З цього правила виходить, що завжди можна перемножувати дві квадратні матриці одного порядку, в результаті одержимо квадратну матрицю того ж порядку. Зокрема, квадратну матрицю завжди можна помножити саму на себе, тобто звести в квадрат.

Іншим важливим випадком є множення матриці-рядка на матрицю-стовпець, причому ширина першої повинна дорівнювати висоті другою, в результаті одержимо матрицю першого порядку (тобто один елемент). Дійсно,

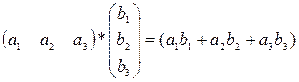
Приклади.

1) Нехай

Знайти елементи c₁₂, c₂₃ і c₂₁ матриці С.

2) Знайдемо добуток матриць.

3) Знайдемо добуток матриць

4) Знайти добуток матриць

– не можна, оскільки ширина першої матриці дорівнює 2-м елементам, а висота другої – 1-му.

5) Нехай Знайти АВ й ВА.

6) Нехай

Знайти АВ і ВА.

ВА – не має сенсу.

Таким чином, ці прості приклади показують, що матриці, взагалі кажучи, не перестановочні одна з одною, тобто AB ¹ BA. Тому при множенні матриць потрібно ретельно стежити за порядком множників.

Можна перевірити, що множення матриць підкоряється асоціативному й дистрибутивному законам, тобто (AB) C=A(BC) й (A+B) C=AC+BC.

Легко також перевірити, що при множенні квадратної матриці А на одиничну матрицю E того ж порядку знов одержимо матрицю А, причому AE=EA=A.

Можна відзначити наступний цікавий факт. Як відомо добуток 2-х відмінних від нуля чисел не рівний 0. Для матриць це може не мати місця, тобто добуток 2-х не нульових матриць може виявитися рівним нульовій матриці.

Наприклад, якщо Тоді

Дата добавления: 2015-07-12