
|
Читайте также: |
Поняття оберненої матриці вводиться тільки для квадратних матриць.
Якщо А – квадратна матриця, то оберненою для неї матрицею називається матриця, що позначається A-1 та задовольняє умові  . (Це визначення вводиться по аналогії з добутком чисел)
. (Це визначення вводиться по аналогії з добутком чисел)
Справедлива наступна теорема:
Теорема. Для того, щоб квадратна матриця А мала обернену, необхідно й достатньо, щоб її визначник був відмінний від нуля.
Якщо умови теореми виконані, то матриця обернена до матриці

знаходиться таким чином
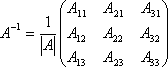 ,
,
де Aij – алгебраїчні доповнення елементів aij даної матриці А.
Отже, щоб знайти обернену матрицю потрібно:
1. Знайти визначник матриці А.
2. Знайти алгебраїчне доповнення Aij всіх елементів матриці А і скласти матрицю 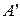 , елементами якої є числа Aij.
, елементами якої є числа Aij.
3. Знайти матрицю, транспоновану одержаній матриці,
і помножити її на  – це й буде
– це й буде  .
.
Визначники та їх властивості
Визначником другого порядку, відповідним даній матриці, називається число, що одержане таким чином:  .
.
Визначник позначається символом  .
.
Отже, для того, щоб знайти визначник другого порядку потрібно з добутку елементів головної діагоналі відняти добуток елементів другої діагоналі.
Приклади. Обчислити визначники другого порядку.
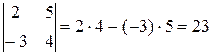 .
.
 .
.
Обчислити визначник матриці D, якщо D= -А+2В й
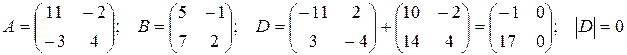
Аналогічно можна розглянути матрицю третього порядку і відповідний їй визначник.
Визначником третього порядку, відповідним даній квадратній матриці третього порядку, називається число, що позначається й одержується таким чином:
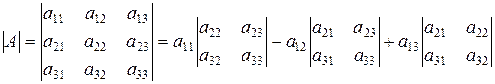
Таким чином, ця формула дає розкладання визначника третього порядку по елементах першого рядка  й зводить обчислення визначника третього порядку до обчислення визначників другого порядку.
й зводить обчислення визначника третього порядку до обчислення визначників другого порядку.
Приклади. 1) Обчислити визначник третього порядку.
 .
.
На відміну від матриці, яка є таблицею чисел, визначник - це число, яке певним чином ставиться у відповідність матриці.
Обчислити визначник

Розв'язання.
2) Обчислимо визначник третього порядку методом трикутника.


Властивості визначників.
1) Визначник не міняється, якщо замінити його рядки стовпцями й навпаки, наприклад, для визначника третього порядку
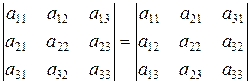 .
.
2) При перестановці 2-х рядків або стовпців визначник змінить знак на протилежний, зберігаючи абсолютну величину, тобто, наприклад,

3) Якщо визначник має два однакові рядки або стовпців, то він дорівнює нулю. Наприклад, 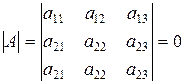 .
.
Дійсно, якщо переставити тут 2-й і 3-й рядки, то за властивістю (2) цей визначник повинен змінити знак, але сам визначник в даному випадку не міняється, тобто одержуємо | A| = –| A | або | A| = 0.
4) Загальний множник рядка або стовпця можна виносити за знак визначника. Наприклад, 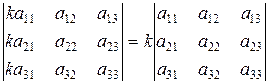 .
.
5) Якщо всі елементи будь-якого рядка або стовпця визначника дорівнюють нулю, то сам визначник дорівнює нулю.
6) Якщо всі елементи будь-якого рядка або стовпця визначника представлені у вигляді суми 2-х елементів, то визначник можна представити у вигляді суми 2-х визначників по формулі, наприклад,

7) Якщо до будь-якого рядка (або стовпця) визначника додати відповідні елементи іншого рядка (або стовпця), помножені на одне і теж число, то визначник не змінить своєї величини. Наприклад,

Ці властивості визначників досить часто використовуються при обчисленні визначників і в різних задачах.
Алгебраїчне доповнення і мінор
Нехай маємо визначник третього порядку:
 .
.
Мінором, відповідним даному елементу аij визначника третього порядку, називається визначник другого порядку, одержаний з даного викреслюванням рядка і стовпця, на перетині яких стоїть даний елемент, тобто i -ой рядка й j -го стовпця. Мінор відповідний даному елементу аij позначатимемо Мij.
Наприклад, мінором М12, відповідним елементу а12, буде визначник  , який отримано викреслюванням з даного визначника 1-го рядку й 2-го стовпця.
, який отримано викреслюванням з даного визначника 1-го рядку й 2-го стовпця.
Таким чином, формула, що визначає визначник третього порядку, показує, що цей визначник рівний сумі добутків елементів 1-го рядка на відповідний мінор; при цьому мінор, відповідний елементу a12, береться із знаком “–”, тобто можна записати, що

Аналогічно можна ввести визначення мінору для визначників другого порядку і вищих порядків.
Введемо ще одне поняття.
Алгебраїчним доповненням елементу аij визначника називається його мінор Мij помножений на (-1)i+j.
Алгебраїчне доповнення елементу аij позначається Аij.
З визначення одержуємо, що зв'язок між доповненням алгебри елементу і його мінором виражається рівністю 
Наприклад, 
Приклад. Запропоновано визначник  . Знайти
. Знайти 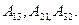 .
.
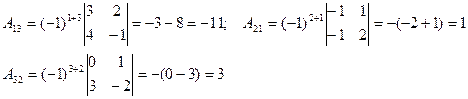
Легко бачити, що використовуючи алгебраїчні доповнення елементів, формулу для обчислення визначників можна записати у вигляді:

Теорема (про розкладання визначника по заданому рядку або стовпцю). Визначник рівний сумі добутків елементів будь-якого його рядку (або стовпця) на їх алгебраїчні доповнення.
Все вищесказане справедливе для визначників будь-якого порядку.
Приклад.
Обчислити визначник 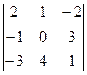 , розкладаючи його по елементах 2-го стовпця.
, розкладаючи його по елементах 2-го стовпця.

Тема 2. Загальна теорія систем лінійних рівнянь.
Системою m лінійних рівнянь з n невідомими називається система вигляду

де aij і bi (i=1,…,m; j=1,…,n) – деякі відомі числа, а x1,…,xn – невідомі. У позначенні коефіцієнтів aij перший індекс i означає номер рівняння, а другий j – номер невідомого, при якому стоїть цей коефіцієнт.
Коефіцієнти при невідомих записуватимемо у вигляді матриці
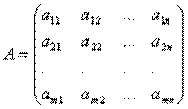
яку назвемо матрицею системи.
Числа, що стоять в правих частинах рівнянь, b1,…,bm називаються вільними членами.
Сукупність n чисел c1,…,cn називається рішенням даної системи, якщо кожне рівняння системи обертається в рівність після підстановки в нього чисел c1,…,cn замість відповідних невідомих x1,…,xn.
Наша задача полягатиме в знаходженні рішень системи. При цьому можуть виникнути три ситуації:
1. Система може мати єдине рішення.
2. Система може мати нескінченну безліч рішень. Наприклад

3. І третій випадок, коли система взагалі не має рішення. Наприклад,

якби рішення існувало, то x1+ x2 дорівнювало б одночасно нулю і одиниці.
Система лінійних рівнянь, що має хоча б одне рішення, називається сумісною. Навпаки, тобто якщо система не має рішень, то вона називається несумісною.
Розглянемо способи знаходження розв’язань системи.
Матричний метод рішення систем лінійних рівнянь
Матриці дають можливість стисло записати систему лінійних рівнянь. Хай дана система з 3-х рівнянь з трьома невідомими
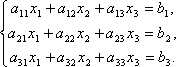
Розглянемо матрицю системи

і матриці стовпці невідомих і вільних членів

Знайдемо добуток

тобто в результаті множення ми одержуємо ліві частини рівнянь даної системи. Тоді, користуючись визначенням рівності матриць, дану систему можна записати у вигляді

або коротше A·X=B.
Тут матриці А і B відомі, а матриця X невідома. Її й потрібно знайти, оскільки її елементи є рішенням даної системи. Це рівняння називають матричним рівнянням.
Хай визначник матриці відмінний від нуля |A| ¹ 0. Тоді матричне рівняння розв'язується таким чином. Помножимо обидві частини рівняння зліва на матрицю A-1, обернену матриці А: A-1(AX)=A-1B або (A-1A)X=A-1B. Оскільки A-1A = E та E·X = X, то одержуємо рішення матричного рівняння у вигляді
X=A-1B.
Зауважимо, що оскільки обернену матрицю можна знайти тільки для квадратних матриць, то матричним методом можна вирішувати тільки ті системи, в яких число рівнянь співпадає з числом невідомих. Проте, матричний запис системи можливий і у разі, коли число рівнянь не дорівнює числу невідомих, тоді матриця А не буде квадратною і тому не можна знайти рішення системи у вигляді X = A-1B.
Приклади. Вирішити системи рівнянь матричним методом
1)

Таким чином, x = 3, у = – 1.
2)

Отже, х1 =4, х2 =3, х3 =5.
3) Вирішіть матричне рівняння: XA+B=C, де

Виразимо шукану матрицю X із заданого рівняння

Знайдемо матрицю А-1.
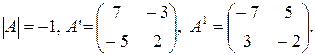
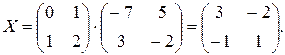
Перевірка:
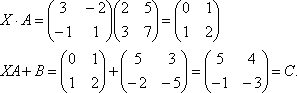
4) Вирішіть матричне рівняння AX+B=C, де
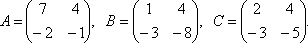
З рівняння одержуємо
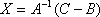
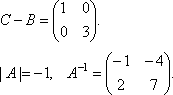
Отже,

Дата добавления: 2015-07-12; просмотров: 279 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Приклади. | | | Правило Крамера |