
Читайте также:
|
1. Обчислити визначники:
1) 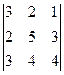 2)
2) 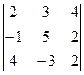
3) 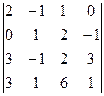 4)
4) 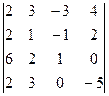
Відповіді: 1) 8; 2) –6; 3) 0; 4) 48.
2. Вирішити систему лінійних рівнянь методом Крамера, Гауса, матричним методом:
1) 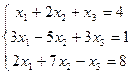 2)
2) 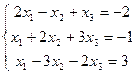
3) 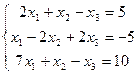 4)
4) 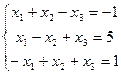
Відповіді: 1) (1;1;1;); 2) немає рішень; 3) (1;5;2); 4) (2;0;3)
Тема 3. Лінії на площині.
Рівнянням лінії (кривій) на площині Оxy називається рівняння, якому задовольняють координати кожної крапки даної лінії й не задовольняють координати будь-якої крапки, що не лежить на цій лінії.
У загальному виді рівняння лінії може бути записане виді 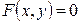 (3.1)
(3.1)
(або якщо це можливо) 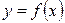 , де
, де 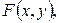
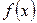 – деякі функції.
– деякі функції.
Якщо крапка 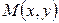 пересувається по лінії, то її координати, змінюючись, задовольняють рівнянню цієї лінії. Тому координати крапки
пересувається по лінії, то її координати, змінюючись, задовольняють рівнянню цієї лінії. Тому координати крапки 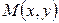 називаються поточними координатами. Букви, що входять у рівняння називаються параметрами.
називаються поточними координатами. Букви, що входять у рівняння називаються параметрами.
Усяке рівняння першого ступеня відносно x і y, тобто рівняння виду
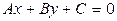 , (3.2)
, (3.2)
де А, В и С – постійні коефіцієнти, причому 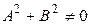 , визначає на площині деяку пряму. Це рівняння називається загальним рівнянням прямої.
, визначає на площині деяку пряму. Це рівняння називається загальним рівнянням прямої.
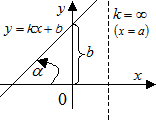 Рівняння
Рівняння 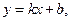 (3.3) називається рівнянням прямої з кутовим коефіцієнтом, де k - кутовий коефіцієнт.
(3.3) називається рівнянням прямої з кутовим коефіцієнтом, де k - кутовий коефіцієнт.
k = tg a, где a - кут нахилу прямої до осі OX.
Якщо пряма задана загальним рівнянням
Ax+By+C=0, то її кутовий коефіцієнт визначається по формулі
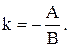 (3.4)
(3.4)
Рівняння y-y0 = k(x-x0) (3.5)
є рівнянням прямої, що проходить через точку M(x0;y0) і що має кутовий коефіцієнт k.
Рівняння 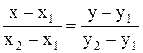 (3.6)
(3.6)
є рівняння прямої, що проходить через две точки M1(x1; y1) і M2(x2; y2).
Ознакою паралельності двох прямих є рівність їх кутових коефіцієнтів k1=k2.
Ознакою перпендикулярності двох прямих є співвідношення
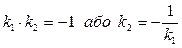 .
.
Приклад. Скласти рівняння прямої, що проходить через точки A(2;3) і B(5;1).
Розв’язок.
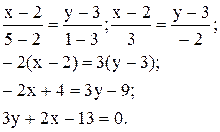
Приклад. Задана пряма 2x+3y+4=0. Скласти рівняння прямої, що проходить через точку M0(2;1):
а) параллельно до даної прямої;
б) перпендикулярно до даної прямої.
Розв’язок. Визначимо згідно з формулою (3.4) кутовий коефіцієнт даної прямої 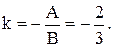
Скласти рівняння прямої, що проходить через точку M0 і що має кутовий коефіцієнт k1:
y-1=k1(x-2).
а) Для того, щоб знайдена пряма y-1=k1(x-2) була паралельною до заданій 2x+3y+4=0 необхідно щоб виконувалась рівність k=k1.
Таким чином, рівняння прямої, що проходить через точку M0 і що є паралельною до заданої, буде мати такий вигляд:
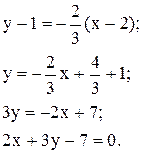
б) Для того, щоб знайдена пряма y-1=k1(x-2) була перпендикулярною до заданої прямої, необхідно щоб виконувалась рівність k × k1= -1
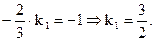
Таким чином, рівняння прямої, що проходить через точку M0 і що є перпендикулярною до заданої прямої, буде таким:
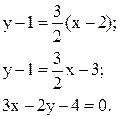
Приклад. Скласти рівняння прямої, що проходить через точку A(2; 3) і є перпендикулярною до прямої 4x+3y-12=0.
Розв’язок. Складемо рівняння прямої, що проходить через точку A(2; 3) під кутом a:
y-3=k2(x-2), де k2=tga.
Кутовий коефіцієнт даної прямої k1=-4/3.
Враховуючи, що кутові коефіцієнти перпендикулярних прямих зв’язані співвідношенням k1×k2=-1, отримуємо -4/3×k2= -1, звідки k2=3/4.
Підставляючи k2 в отримане рівняння, випишемо рівняння прямої
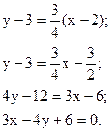
Рівняння прямої "у відрізках"
Якщо жоден з коефіцієнтів рівняння (3.2) не дорівнює нулю, то його можна перетворити до вигляду
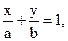 (3.7)
(3.7)
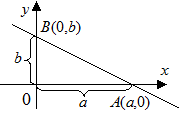 де -
де - 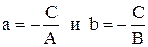 - величини відрізків, які відтинає пряма на координатних осях.
- величини відрізків, які відтинає пряма на координатних осях.
Це рівняння (3.7) називається рівнянням прямої "у відрізках". Цим рівнянням користуються для побудови прямої. Тому при необхідності рівняння прямої призводять до виду рівняння "у відрізках" і будують пряму.
Приклад. Побудувати пряму 5x-3y = -15.
Розв’язок.
Перетворимо це рівняння в рівняння прямої в "відрізках". Для цього розділимо обидві частини рівняння на -15. Отримаємо
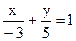
На осі абсцис відкладаємо відрізок, величина якого дорівнює a = -3 одиниці, на осі ординат b = 5 одиниць і з'єднаємо їх кінці.
Рівняння прямої, що проходить через дану точку M1(x1;y1) і має заданий нормальний вектор:
A(x-x1)+B(y-y1)=0 (3.8)
Будь-який ненульовий вектор 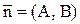 , перпендикулярний даній прямій, називається нормальним вектором цієї прямої.
, перпендикулярний даній прямій, називається нормальним вектором цієї прямої.
Приклад. Скласти рівняння прямої, що проходить через точку M1(2; 3) і що має нормальний вектор 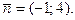
Розв’язок. Запишемо рівняння шуканої прямий, підставивши дані в (3.8):
-1(x-2)+4(y-3)=0;
-x+2+4y-12=0;
x-4y+10-0.
Будь-який ненульовий вектор 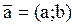 , колінеарний даній прямій, називається направляючим вектором цієї прямої. Рівняння прямої, що проходить через дану точку M1(x1, y1) і має заданий направляючий вектор, має вигляд:
, колінеарний даній прямій, називається направляючим вектором цієї прямої. Рівняння прямої, що проходить через дану точку M1(x1, y1) і має заданий направляючий вектор, має вигляд:
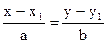 (3.9)
(3.9)
Приклад. Скласти рівняння прямої, що проходить через точку А(2; -1) і що має направляючий вектор 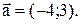
Розв’язок. Підставимо дані свого приклада в (3.9) і отримаємо:
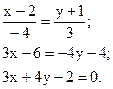
Паралельність прямих
Нехай на площі задані дві прямі
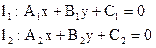
нормальні вектори цих прямих мають координати
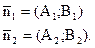
Якщо l1 êêl2, то їх нормальні вектори колінеарні Þ 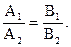
Якщо 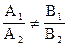 , то прямі різні, не паралельні одна одній, а значить перетинаються в одній точці (l1Il2).
, то прямі різні, не паралельні одна одній, а значить перетинаються в одній точці (l1Il2).
Якщо 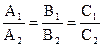 , то обидва рівняння визначають одну й ту ж пряму l1=l2.
, то обидва рівняння визначають одну й ту ж пряму l1=l2.
Приклад. Установити, чи паралельні прямі?
а) 4x-6y+10=0
6x-9y+2=0.
Розв’язок. Складемо співвідношення
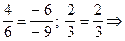 прямі паралельні;
прямі паралельні;
б) 6x-3y-2=0
4x-10y+6=0.
Розв’язок: 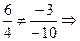 прямі не паралельні.
прямі не паралельні.
Перпендикулярність прямих
Якщо l1^l2, то скалярний добуток нормальних векторів цих прямих повинен бути рівний нулю, тобто 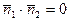 A1A2+B1B2=0.
A1A2+B1B2=0.
Приклад. Установити, чи перпендикулярні прямі?
5x-2y+1=0
4x+10y-1=0.
Розв’язок.
5×4+(-2)×10=0
20-20=0 Þ прямі перпендикулярні.
Кут між двома прямими
Кутом між двома прямими називається величина меншого з кутів, створеного цими прямими.
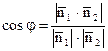 , (3.10)
, (3.10)
де 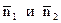 - нормальні вектори прямих l1 і l2
- нормальні вектори прямих l1 і l2
Приклад. Найти кут між двома прямими
2x-3y+4=0 і x+5y-3=0.
Розв’язок. Найдемо координати нормальних векторів заданих прямих:
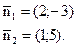
Тепер скористаємося формулою (3.10)
Кут між прямою і площиною.
Нехай задані пряма 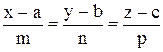 з направляючим вектором
з направляючим вектором 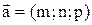 і площина Ax+By+Cz+D=0 з нормальним вектором
і площина Ax+By+Cz+D=0 з нормальним вектором 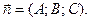
Кут між прямою і площиною - це кут між цією прямою та її проекцією на цю площину:
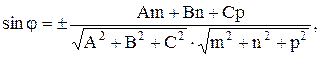 (3.11)
(3.11)
якщо “+” - кут гострий;
якщо “-“ - кут тупий.
Приклад. Найти гострий кут між прямою
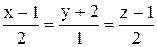 і площиною 2x+y-z+4=0.
і площиною 2x+y-z+4=0.
Розв’язок. Направляючий вектор прямої:
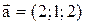 .
.
Нормальний вектор площини:
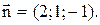
Підставив ці координати в (3.11) маємо
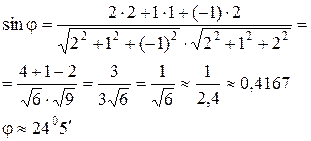
Умови паралельності і перпендикулярності прямої і площі
Умови паралельності прямої 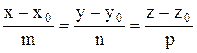 та
та
площі Ax+By+Cz+D=0 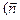 ^
^ 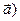 :
:
Am+Bn+Cp=0 (3.12)
Умова перпендикулярності прямої і площі
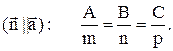

 (3.13)
(3.13)
Відстань від крапки до прямої
Нехай дані крапка 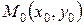 й пряма
й пряма 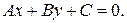
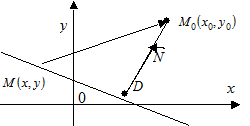 Під відстанню d від крапки М0 до прямої АВ розуміється довжина перпендикуляра M0D, опущеного із крапки M0 на пряму АВ.
Під відстанню d від крапки М0 до прямої АВ розуміється довжина перпендикуляра M0D, опущеного із крапки M0 на пряму АВ.
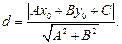 (3.14)
(3.14)
Приклад. Знайти відстань між паралельними прямими 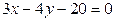 й
й 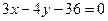 .
.
Рішення. Поберемо на одній із прямих, наприклад на прямій 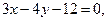 довільну крапку Е (12,0). Тоді шукана відстань дорівнює відстані від крапки Е до прямої
довільну крапку Е (12,0). Тоді шукана відстань дорівнює відстані від крапки Е до прямої 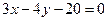 :
: 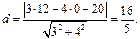 .
.
Завдання для самоконтроля.
1. Найти рівняння площі, що проходить через точку Р(2; -4; -2) перпендикулярно прямій
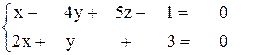
Відповідь: 5x-10y-9z-68=0.
2. Найти рівняння прямої, що проходить через точку А(2; 1; 6) і перпендикулярна площі
x-4y+5z-1=0
Відповідь: 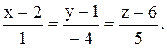
Взаємне розташування прямої і площі.
Нехай задані площа Ax+By+Cz+D=0 і пряма 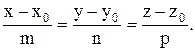
Для визначення точки перетину рівняння прямої записують в параметричній формі 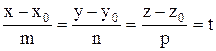
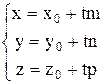 (3.15)
(3.15)
Після ці x, y, z підставляють в рівняння площі:
A(x0+tm)+B(y0+tn)+C(z0+tp)+D=0, або
Ax0+By0+Cz0+t(Am+Bn+Cp)+D=0,
звідки
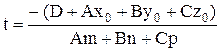 . (3.16)
. (3.16)
Приклад. Задані пряма 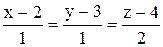 і площа 2x+y+z-6=0. Найти точку їх перетину.
і площа 2x+y+z-6=0. Найти точку їх перетину.
Розв’язок. Запишемо рівняння прямої в параметричній формі
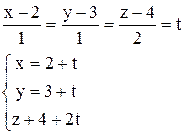 (*)
(*)
Підставляємо ці x, y, z в рівняння даної площі
2(2+t)+(3+t)+(4+2t)-6=0;
4+2t+3+t+4+2t-6=0;
5t+5=0; t=-1.
Підставимо отримані значення t в (*), тим самим найдемо координати точки перетину заданих прямої і площі:
x=2-1=1;
y=3-1=2;
z=4-2=2.
Відповідь: (1; 2; 2).
Тема 4. Криві другого порядку
1. Еліпс.
Еліпс представляє собою результат рівномірної деформації окружності уздовж одного з її діаметрів.
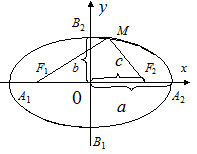 Еліпсом називається геометричне місто точок, для яких сума відстань від двох фіксованих точок площі, званих фокусами, є постійна величина.
Еліпсом називається геометричне місто точок, для яких сума відстань від двох фіксованих точок площі, званих фокусами, є постійна величина.
F1 и F2 – фокуси еліпса, F1(-c; 0); F2(c;0).
Відстань між ними - 2С.
Візьмемо довільну точку еліпса M(x, y). Обозначимо F1M=r1 F2M=r2.
Тоді F1M+F2M=r1+r2=2a, де
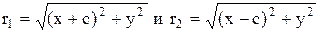 - фокальні радіуси точки М.
- фокальні радіуси точки М.
Канонічне рівняння еліпса:
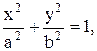 (4.1)
(4.1)
де b2=a2-c2.
Це рівняння другого ступеня Þ еліпс є лінія другого порядку. Еліпс симетричний відносно обох осей координат.
Ексцентриситетом еліпса називається відношення відстані між фокусами до довжини великий осі
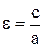 (4.2)
(4.2)
Так як c<a, то e<1.
Ексцентриситет характеризує форму еліпса. Чим більше ексцентриситет, тим більше еліпс витягнутий (у разі окружності b =a і e=0).
Дві прямі, перпендикулярні до великої осі еліпса і розташовані симетрично щодо центру на відстані 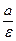 від нього, називаються директрисами еліпса.
від нього, називаються директрисами еліпса.
Рівняння директрис: 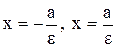 , (4.3)
, (4.3)
Приклад 1. Знайти півосі, координати фокусів і ексцентриситет еліпса
x2+2y2=8.
Розв’язок. Приведемо рівняння еліпса до канонічного виду, для цього розділимо обидві частини рівняння на 8:
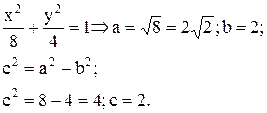
Таким чином
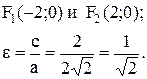
Приклад 2. Написати канонічне рівняння еліпса, довжина малої осі якого дорівнює 6, а фокусна відстань дорівнює 8: 2b=6; 2c=8.
Розв’язок:
2b=6 Þ b=3
Відомо, що 2c=8 Þ c=4.
a2=b2+c2; a2=9+16=25,
запишемо рівняння еліпса 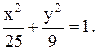
Завдання для самоконтролю.
1. Дан еліпс 9x2+25y2=225.
Знайти: 1) його півосі;
2) фокуси;
3) ексцентриситет;
4) рівняння директриси.
Відповідь: 1) 5 и 3;
2) F1(-4; 0) и F2(4; 0);
3) e=4/5;
4) x=±25/4.
2. Скласти рівняння еліпса, знаючи, що
1) його велика вісь дорівнює 10, а відстань між фокусами 2с=8;
2) його мала вісь дорівнює 6, а відстань між директрисами дорівнює 13;
3) його велика вісь дорівнює 20, а ексцентриситет e=3/5.
Відповідь: 1) 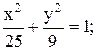
2) 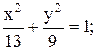
3) 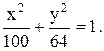
2. Гіпербола.
Гіперболою називається геометричне місце точок, для яких різниця відстаней від двох фіксованих точок площині, званих фокусами, є постійна величина.
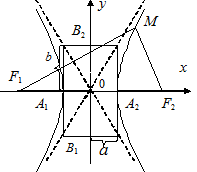
| F1(-c; 0) и F2(c;0) – фокуси;
М(x, y) довільна точка гіперболи.
F1M=r1; F2M =r2 - фокальні радіуси F1F2=2c;
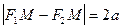 , ,
|
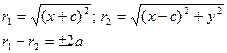
Канонічне рівняння гіперболи:
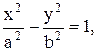 (4.4)
(4.4)
де b2=c2-a2.
Гіпербола - лінія другого порядку, симетрична щодо осей координат.
Ексцентриситетом гіперболи називається відношення відстані між фокусами цієї гіперболи до відстані між її вершинами.
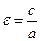 (4.5)
(4.5)
так як c>a, то e>1.
Прямокутник із сторонами 2а і 2b, розташований симетрично щодо осей гіперболи і торкається її в вершинах (A1 і A2), називається основним прямокутником гіперболи.
Ексцентриситет гіперболи характеризує форму її основного прямокутника, а значить, і форму гіперболи: чим менше ексцентриситет, тим більше витягнутий основний прямокутник.
Дві прямі, перпендикулярні до тієї осі гіперболи, яка її перетинає, і розташовані симетрично щодо центру на відстані 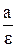 від нього, називаються директрисами гіперболи.
від нього, називаються директрисами гіперболи.
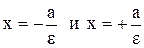 (4.6)
(4.6)
Гілки гіперболи (2.1) як завгодно близько наближаються до прямих
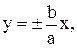 (4.7)
(4.7)
які називаються асимптотами гіперболи.
Дві гіперболи, які визначаються рівняннями
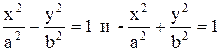
називаються сполученими.
Гіпербола з рівними півосями (a = b) називається рівнобічною; її канонічне рівняння має вигляд x2-y2=a2 або -x2+y2=a2.
Приклад 1. Дана гіпербола 16x2-9y2=144.
Знайти: 1) півосі a і b;
2) фокуси;
3) ексцентриситет;
4) рівняння асимптот;
4) рівняння директриси.
Розв’язок.
1) Приведемо рівняння гіперболи до канонічного виду, розділивши обидві частини рівняння на 144. Отримаємо:
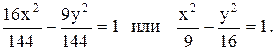
Тоді a=3; b=4.
2) Знаючи півосі a і b, можемо знайти c зі співвідношення
b2=c2-a2
16=c2-9
c2=25
c=5.
Тоді фокуси даної гіперболи мають координати
F1(-5,0) і F2(5,0).
3) Ексцентриситет тепер легко визначити за формулою (4.5) 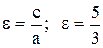 .
.
4) Рівняння асимптот по (4.7)
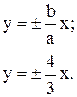
5) Рівняння директрис по (4.6)
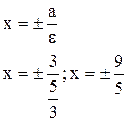
Приклад 2. Скласти рівняння гіперболи, фокуси якої розташовані на осі абсцис симетрично відносно початку координат, знаючи, крім того, що: її осі 2а=10 і 2b=8;
1) відстань між фокусами 2с=10 і ось 2b=8;
2) відстань між фокусами 2с=6 і ексцентриситет e=3/2;
3) ось 2а=16 і ексцентриситет e=5/4;
4) рівняння асимптот y=±4/3x і відстань між фокусами 2с=20;
5) відстань між директрисами дорівнює 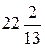 і відстань між фокусами 2с=26.
і відстань між фокусами 2с=26.
Розв’язок:
1) 2а=10 і 2b=8. Звідки а=5; b=4.
Рівняння гіперболи: 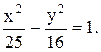
2) 2с=10 и 2b=8. Þ c=5; b=4.
З b2=c2-a2 знайдемо a:
16=25-а2; а2=25-16
а2=9; а=3.
Рівняння гіперболи: 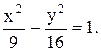
3) 2с=6 и e=3/2.
c=3;
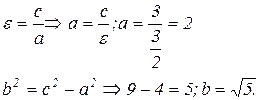
Рівняння гіперболи: 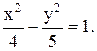
4) 2а=16 и e=5/4
а=8 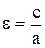 Þ 5/4 = c/8 Þ c=10
Þ 5/4 = c/8 Þ c=10
b2=c2-a2=100-64=36; b=6
Рівняння гіперболи: 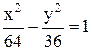
5) 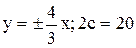
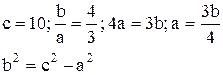
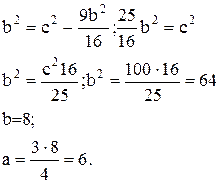
Рівняння гіперболи: 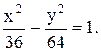

6) 2с=26; 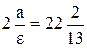 ;
;
с=13; 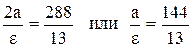
13а=144e, а e= 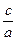
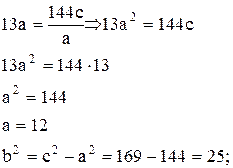
Рівняння гіперболи: 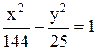 .
.
Завдання для самоконтролю.
1. Дана гіпербола 9x2-16y2=36
знайти:
1) півосі a і b;
2) фокуси;
3) ексцентриситет;
4) рівняння асимптот;
5) рівняння директриси.
Відповіді:
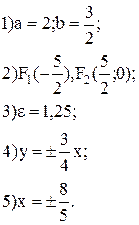
2. Скласти рівняння гіперболи, якщо відстань між директрисами дорівнює 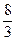 і ексцентриситет
і ексцентриситет 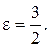
Відповідь: 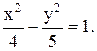
3. Скласти рівняння гіперболи, якщо рівняння асимптот 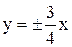 і відстань між директрисами дорівнює
і відстань між директрисами дорівнює 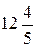 .
.
Відповідь: 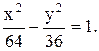
Дата добавления: 2015-07-12; просмотров: 165 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Метод Гауса | | | Парабола. |