
Читайте также:
|
Знайти границі функцій:
1.  2.
2. 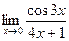 3.
3.  4.
4.  5.
5. 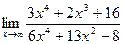 6.
6.  7.
7.  8.
8.  9.
9. 
| 10.  11.
11. 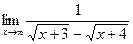 12.
12.  13.
13.  14.
14. 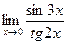 15.
15.  16.
16. 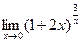 17.
17. 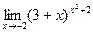 18.
18. 
|
Відповіді: 1) 0; 2) 1; 3) 1,8; 4)  ; 5) 0,6; 6) –0,6; 7)
; 5) 0,6; 6) –0,6; 7)  ; 8) 0; 9) 1,6; 10) 3; 11)
; 8) 0; 9) 1,6; 10) 3; 11) 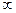 ; 12) 0,5;
; 12) 0,5;
13) 7; 14) 1,5; 15) 4/9; 16) е6; 17) е2; 18) е3.
Тема 6. Неперервність функції
Уявлення про неперервність функції інтуїтивно пов'язане у нас з тим, що її графіком є плавна лінія, що ніде не переривається. При розгляді графіка такої функції у = f(x) ми бачимо, що близьким значенням аргументу відповідають близькі значення функції: якщо незалежна змінна x наближається до точки x0, то значення функції у = f(x) необмежено наближається до значення функції в точці x0, тобто до f(x0).
Дамо визначення безперервності функції. Отже, хай маємо функцію у = f(x).
Функція у=f(x) називається неперервною в точці x0, якщо вона визначена в цій точці і в деякому околі, що містить x0 та
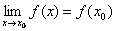
Таким чином, можна сказати, що функція безперервна в точці x0, якщо виконані 3 умови:
1) вона визначена в точці x0 і в деякому його околі;
2) має границю при x ® x0;
3) ця границя дорівнює значенню функції в точці x0.
Формулу (1) можна записати у вигляді 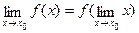 , оскільки
, оскільки  . Це означає, що для того, щоб знайти границю безперервної функції при x® x0, достатньо у вираз функції підставити замість аргументу x його значення x0.
. Це означає, що для того, щоб знайти границю безперервної функції при x® x0, достатньо у вираз функції підставити замість аргументу x його значення x0.
Приклад: Доведемо, що функція y = 3 x 2 неперервна в довільній точці x0. Для цього знайдемо  .
.
Якщо функція y=f(x) неперервна в кожній точці деякого інтервалу (а; b), де а < b, то говорять, що функція неперервна на цьому інтервалі.
Неперервні функції мають наступні властивості.
Теорема 1. Якщо функції f(x) і g(x) безперервні в точці x0, то їх сума φ(x)= f(x)+ g(x) також є неперервна функція в точці x0.
Теорема 2. Добуток двох неперервних функцій є функція неперервна.
Теорема 3. Частка двох неперервних функцій є функція неперервна, якщо знаменник в даній точці не обертається в нуль.
Якщо функцію можна представити у вигляді у = f(u), де u = φ(x), тобто якщо функція у залежить від змінної х через проміжний аргумент u, то у називається складною функцією змінної x.
Приклади:
у = sinx3. Тут u = x3, у = sin u.
у = etg x, u = tg x, у = eu.
Таким чином, під терміном "складна функція" треба розуміти не будь-який дуже складний вираз, а функцію, яка залежить від аргументу x через декілька проміжних функцій.
Теорема 4. Якщо функція u = φ(x) неперервна в точці x0 і приймає в цій точці значення u0 = φ(x0), а функція f(u) неперервна в точці u0, то складна функція y = f(φ(x)) неперервна в точці x0.
Використовуючи ці теореми можна довести наступний результат.
Теорема 5. Будь-яка елементарна функція неперервна в кожній точці, в якій вона визначена.
Зазначимо, що якщо функція у = f(x) неперервна в точці x0 і її значення в цій точці відмінне від 0 (f(x0) ≠ 0), то значення функції f(x) в деякому околі точки x0 мають той самий знак, що і f(x0), тобто якщо f(x0) > 0, то знайдеться таке δ > 0, що на інтервалі (x0 – δ; x0+ δ) f(x) > 0 (у цьому околі значення функції f(x) дуже мало відрізняються від своєї границі).
Точки розриву і їх класифікація
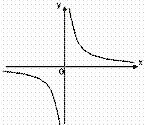
 Якщо розглянути графік функції
Якщо розглянути графік функції  у околиці точки x= 0 (див. рис. справа), то ясно видно, що він як би “розривається” на окремі криві. Аналогічно можна розглянути функцію, зображену на рисунку зліва в околі точки 2. Говорять, що у всіх вказаних точках відповідні функції стають розривними.
у околиці точки x= 0 (див. рис. справа), то ясно видно, що він як би “розривається” на окремі криві. Аналогічно можна розглянути функцію, зображену на рисунку зліва в околі точки 2. Говорять, що у всіх вказаних точках відповідні функції стають розривними.
Точка x0 називається точкою розриву функції у = f(x), якщо вона належить області визначення функції або її границі і не є точкою неперервності.
В цьому випадку говорять, що при x= x0 функція розривна. Це може відбутися, якщо в точці x0 функція не визначена або не існує межа 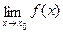 , або якщо межа існує, але
, або якщо межа існує, але  .
.
Приклади.
Розглянемо функцію:

Ця функція визначена в усіх точках відрізка [0, 4] і її значення при x= 3 дорівнює 0. Проте, в точці x= 3 функція має розрив, оскільки вона не має границі при x=3:

Слід зазначити, що f(x) неперервна у всій решті точок відрізка [0, 4]. При цьому в точці x= 0 вона неперервна справа, а в точці x= 4 – зліва, оскільки
 .
.
Як вже наголошувалося, функція  розривна при x = 0. Дійсно, при x = 0 функцію не визначено:
розривна при x = 0. Дійсно, при x = 0 функцію не визначено:  .
.
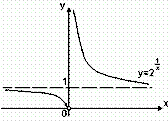 Функція
Функція 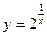 розривна при x = 0. Дійсно,
розривна при x = 0. Дійсно, 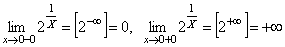 . При x = 0 функцію не визначено.
. При x = 0 функцію не визначено.
Функція 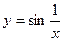 визначена для всіх значень x, окрім x = 0. У цій точці вона має розрив, оскільки границя не існує.
визначена для всіх значень x, окрім x = 0. У цій точці вона має розрив, оскільки границя не існує.
Точки розриву функції можна розбити на два типи.
Точка розриву x0 функції f(x) називається точкою розриву першого роду, якщо існують обидві односторонні кінцеві границі 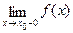 і
і  , але вони не рівні між собою або не рівні значенню функції в точці x0, тобто f(x0). Точка розриву, що не є точкою розриву першого роду, називається точкою розриву другого роду.
, але вони не рівні між собою або не рівні значенню функції в точці x0, тобто f(x0). Точка розриву, що не є точкою розриву першого роду, називається точкою розриву другого роду.
Приклади:
У першому прикладі точка х=3 є точкою розриву першого роду. У  прикладах 2 – 4 всі точки розриву є точками розриву другого роду.
прикладах 2 – 4 всі точки розриву є точками розриву другого роду.
Для функції, зображеної на малюнку точка x = 2 є точкою розриву першого роду.
Функція  не визначена в точці x = 0. Ця точка є точкою розриву 1-го роду, оскільки в ній існують межі справа і зліва.
не визначена в точці x = 0. Ця точка є точкою розриву 1-го роду, оскільки в ній існують межі справа і зліва.
Завдання до самоконтролю.
1. Визначити точки розриву, якщо вони існують:
а)  б)
б)  в)
в) 
2. Визначити вид розриву функції у вказаних крапках:
а)  при х=2 б)
при х=2 б)  при х=0
при х=0
Відповіді: 1а) х=-4, другого роду; б) х=-1, другого роду; у) х1=1, х2=-2, другого роду.
2а) точка розриву першого роду; б) точка розриву першого роду.
Тема 7. Похідна функції
Похідною даної функції у = f(x) в точці x0 називається границя відношення приросту функції Δy до приросту аргументу Δx, коли останнє довільним чином прагне до нуля. Помітимо, що для однієї і тієї ж функції похідна в різних точках x може приймати різні значення, тобто похідну можна розглядати як функцію аргументу x. Ця функція позначається f '(x)
Конкретне значення похідної при x = а позначається f '(a) або у'|x=a. Операція знаходження похідної від функції f(x) називається диференціюванням цієї функції.
Для безпосереднього знаходження похідної за визначенням можна застосувати наступне практичне правило:
1. Додати x приріст Δx і знайти нарощене значення функції f(x + Δx).
2. Знайти приріст функції Δy = f(x + Δx) – f(x).
3. Скласти відношення  та знайти границю цього відношення при Δx ® 0.
та знайти границю цього відношення при Δx ® 0.
Приклади.
Знайти похідну функції у = x2
а) у довільній точці;
б) у точці x= 2.
Розв’язання.
а) f(x + Δx) = (x + Δx) 2;
Δy = (x + Δx)2 – x2=2xΔx– x 2;
 .
.
б) f '(2) = 4
Основні правила диференціювання
Застосовуючи загальний спосіб знаходження похідної за допомогою границі можна одержати прості формули диференціювання. Нехай u=u(x), v=v(x) – дві функції від змінної x., що диференціюються,
1. 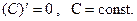
2.. 
3. 
4.  .
.
5.  .
.
6. а)  .
.
б)  .
.
Дата добавления: 2015-07-12; просмотров: 125 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Друга визначна границя | | | Приклади. |