Завдання до самоконтролю

Знайти похідну 2-го порядку.

1.		2.
3.		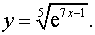4.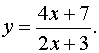
5.		6.
7.		8.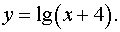
9.		10.

Тема 8. Диференціал функції однієї змінної

Якщо функція y=f(x) має похідну f '(x) у точці x, то добуток похідної f '(x) на приріст Δx аргументу називають диференціалом функції і позначають:

dy = f '(x)·Δ x

Знайдемо диференціал функції y= x. В цьому випадку у'=(x)'= 1 і, отже, dy=dx= Δ x. Таким чином, диференціал dx незалежної змінної x співпадає з її приростом Δx. Тому формулу для диференціала можемо записати так:

dy = f '(x) dx

Приклад. Знайти диференціал функції

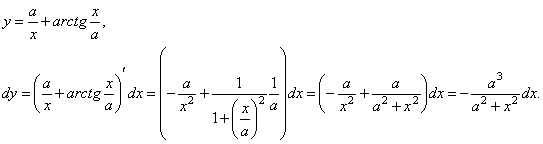
Теорема. Диференціал складної функції y=f(u), для якої u=g(x), має той же вид dy=f'(u) du, який він мав би, якби проміжний аргумент u був незалежною змінною.

Інакше кажучи, форма диференціала не залежить від того, чи є аргумент функції незалежною змінною або функцією іншого аргументу. Ця властивість диференціала називається інваріантністю форми диференціала.

Приклад.

Дана функція. Знайти dy.

Враховуючи властивість інваріантності диференціала, знаходимо

Тема 9. Основні теореми диференціального числення

Правило Лопіталя. Розкриття невизначеностей 0/0 і .

Теорема (правило Лопіталя). Нехай функції f(x) і g(x) є диференційованими в деякому околі точки а, за виключенням, мабуть, самої точки а, і нехай або . Тоді, якщо існує границя відношення похідних цих функцій , то існує і границя відношення самих функцій f(x) /g(x) при x → а, причому

Таким чином, коротко правило Лопіталя можна сформулювати таким чином: границя відношення двох нескінченно малих або двох нескінченно великих величин дорівнює границі відношення їх похідних.

Зауваження. Відзначимо, що ця формула справедлива тільки в тому випадку, якщо границя, що стоїть справа, існує. Може трапитися, що границя, що стоїть зліва існує, тоді як границя, що стоїть в правій частині рівності, не існує.

Наприклад, знайти . Ця границя існує . Але відношення похідних (1+cosx) /1=1+cos xпри x → ∞ не прагне ні до якої границі.

Помітимо, що якщо відношення похідних знову є невизначеністю вигляду 0/0 або , то можна знову застосувати сформульовану теорему, тобто перейти до відношення других похідних і так далі.

Дата добавления: 2015-07-12