Друга визначна границя

Друга визначна границя служить для розкриття невизначеності 1·∞ і виглядає таким чином

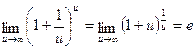
Звернемо увагу на те, що у формулі для другої визначної границі в показнику ступеня повинен стояти вираз, зворотний тому, що додається до одиниці в основі (оскільки в цьому випадку можна ввести заміну змінних і звести шукану границю до другої визначної границі).

Приклади.

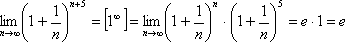
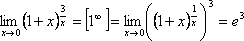
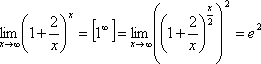
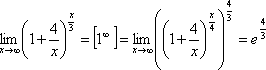
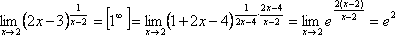
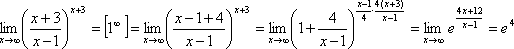
Порівняння нескінченно малих функцій

Нехай при x®a функції f(x) і g(x) є нескінченно малими. Тоді користуватимемося наступними визначеннями.

Якщо 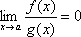, то f(x) називається нескінченно малою вищого порядку, ніж g(x) (щодо g(x)).

Якщо 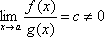, то функції f(x) і g(x) називаються нескінченно малими одного порядку.

Якщо 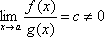, то f(x) називається нескінченно малою к-го порядку щодо g(x).

Якщо 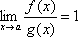, то функції f(x) і g(x) називаються еквівалентними нескінченно малими. В цьому випадку обидві функції прагнуть до нуля приблизно з однаковою швидкістю. Еквівалентні нескінченно малі позначатимемо f(х) ≈ g(х).

Нехай f(x)=x ²–4, g(x)=x²–5x+6 – нескінченно малі при x®2.

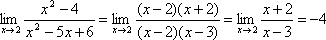
Тому f(x) і g(x) одного порядку.

f(x)=tg2x, g(x) = 2x – нескінченно малі при х®0.

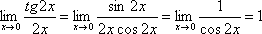
Отже, f ≈ g.

При обчисленні границь корисно пам'ятати про наступну властивість еквівалентних нескінченно малих функцій

Можна довести еквівалентність наступних нескінченно малих функцій при x →0: sin x ≈ x, tg x ≈ x, arcsin x ≈ x, arctg x ≈ x, 1–cos x ≈ x ²∕2, log _a (1+ x) ≈ x/ ln a, ln (1+ x) ≈ x, (1+ x)^m–1 ≈ mx, a^x–1 ≈ xlna, e^x–1 ≈ x.

Дата добавления: 2015-07-12