Приклади. Циклова комісія з математичної та природничо-наукової підготовки

КОЛЕДЖ

ЦИКЛОВА КОМІСІЯ З МАТЕМАТИЧНОЇ ТА ПРИРОДНИЧО-НАУКОВОЇ ПІДГОТОВКИ

ВИЩА МАТЕМАТИКА

Методичні рекомендації

до практичних занять і самостійної роботи

для студентів економічних спеціальностей

Макіївка – 2014

ЗМІСТ

ВСТУП.. 3

МОДУЛЬ 1. ЛІНІЙНА АЛГЕБРА ТА АНАЛІТИЧНА ГЕОМЕТРІЯ.. 4

Тема 1. Елементи теорії матриць і визначників. 4

Тема 2. Загальна теорія систем лінійних рівнянь. 15

Тема 3. Лінії на площині. 22

Тема 4. Криві другого порядку. 30

1. Еліпс. 30

2. Гіпербола. 32

3. Парабола. 37

МОДУЛЬ 2. ОСНОВИ ДИФЕРЕНЦІАЛЬНОГО ЧИСЛЕННЯ.. 39

Тема 5. Границі функції 39

Тема 6. Неперервність функції 49

Тема 7. Похідна функції 52

Тема 8. Диференціал функції однієї змінної 60

Тема 9. Основні теореми диференціального числення. 61

Тема10. Диференційованість функції багатьох змінних. 71

Тема 11. Дослідження функції багатьох змінних на екстремум. Умовний екстремум. 72

МОДУЛЬ 3. ІНТЕГРАЛЬНЕ ЧИСЛЕННЯ ТА ДИФЕРЕНЦІАЛЬНІ РІВНЯННЯ.. 73

Тема 12. Невизначеній інтеграл. 73

Тема 13. Визначений інтеграл. 79

Тема 14. Диференціальні рівняння першого порядку. 82

ЗАВДАННЯ ДО САМОСТІЙНОЇ РОБОТИ СТУДЕНТІВ.. 88

Завдання до 1 модулю.. 88

Завдання до 2 модулю.. 92

Завдання до 3 модулю.. 97

НАВЧАЛЬНО-МЕТОДИЧНА ЛІТЕРАТУРА.. 99

ВСТУП

Мета дисципліни “Вища математика” – ознайомлення студентів з основами математичного апарату, необхідного для розв’язання теоретичних і практичних економічних задач, набуття навичок математичного дослідження прикладних питань економічного напряму.

Основними завданнями курсу є:

– осмислення ролі та місця вищої математики у аналітичних дослідженнях економічних задач;

– вміння формалізувати економічні задачі, обирати та застосовувати методики їх адекватної математичної обробки;

– вміння давати адекватну фахову інтерпретацію на основі одержаних аналітичних результатів.

Знання, набуті при вивченні вищої математики, є основою для вивчення теорії ймовірностей та математичної статистики. Крім того, ознайомлення з основними темами курсу дає додаткові можливості для використання обчислювальної техніки, сприяє розвитку аналітичних навичок та становить основу для практичної формалізованої обробки результатів економічних досліджень.

Предмет дисципліни – вивчення елементів лінійної алгебри, аналітичної геометрії, вступ до математичного аналізу, диференціальне числення функції однієї змінної, інтегральне числення, функції багатьох змінних, звичайні диференціальні рівняння.

Дисципліна є базовою для економічних спеціальностей. Вивчення дисципліни ведеться у формі лекцій, практичних занять та самостійної роботи студентів. Передбачається контроль знань студентів у вигляді завдань до самостійної роботи студентів, тестування, контрольних робіт, екзамену.

МОДУЛЬ 1. ЛІНІЙНА АЛГЕБРА ТА АНАЛІТИЧНА ГЕОМЕТРІЯ

Тема 1. Елементи теорії матриць і визначників.

Основні поняття

Матрицею розміром m ´ n називається сукупність m·n чисел, розташованих у вигляді прямокутної таблиці з m рядків і n стовпців. Цю таблицю зазвичай беруть в круглі дужки. Наприклад, матриці можуть мати вигляд:

Скорочено матрицю можна позначати однією заголовною буквою, наприклад А,або В.

У загальному вигляді матрицю розміром m ´ n записують так

.

Числа, що становлять матрицю, називаються елементами матриці. Елементи матриці зручно позначати двома індексами : перший вказує номер рядка, а другий – номер стовпця. Наприклад, a₂₃ – елемент стоїть в 2-у рядку, 3-у стовпці.

Якщо в матриці число рядків дорівнює числу стовпців, то матриця називається квадратною, причому число її рядків або стовпців називається порядком матриці. У наведених вище прикладах квадратними є друга матриця – її порядок дорівнює 3, і четверта матриця – її порядок 1.

Матриця, в якій число рядків не дорівнює числу стовпців, називається прямокутною. У прикладах це перша матриця і третя.

Розрізняються також матриці, що мають тільки один рядок або один стовпець.

Матриця, у якої всього один рядок , називається матрицею – рядком (або рядковою), а матриця, у якої всього один стовпець, матрицею – стовпцем.

Матриця, всі елементи якої рівні нулю, називається нульовою і позначається (0), або просте 0. Наприклад,

.

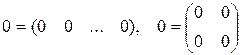Головною діагоналлю квадратної матриці назвемо діагональ, що йде з лівого верхнього в правий нижній кут.

.

Квадратна матриця, у якої всі елементи, що лежать нижче за головну діагональ, рівні нулю, називається трикутною матрицею.

Квадратна матриця, у якої всі елементи, окрім тих, що стоять на головній діагоналі, рівні нулю, називається діагональною матрицею. Наприклад, або .

Діагональна матриця, у якої всі діагональні елементи дорівнюють одиниці, називається одиничною матрицею і позначається буквою E. Наприклад, одинична матриця 3-го порядку має вигляд .

Дії над матрицями

Рівністьматриць. Дві матриці А і B називаються рівними, якщо вони мають однакове число рядків і стовпців і їх відповідні елементи рівні .

Наприклад, нехай й . Тоді можна стверджувати, що A=B, якщо .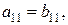

Транспонування. Розглянемо довільну матрицю А з m рядків і n стовпців. Їй можна зіставити таку матрицю B з n рядків і m стовпців, у якої кожен рядок є стовпцем матриці А з тим же номером (отже, кожен стовпець є рядком матриці А з тим же номером).

Отже, якщо то .

Цю матрицю B називають транспонованою матрицею А, а перехід від А до B - транспонуванням.

Таким чином, транспонування – це зміна ролями рядків і стовпців матриці. Матрицю, транспоновану до матриці , звичайно позначають .

Зв'язок між матрицею А та її транспонованою можна записати у вигляді .

Наприклад. Знайти матрицю транспоновану до даної.

,

Додавання матриць. Хай матриці А і B складаються з однакового числа рядків і однакового числа стовпців, тобто мають однакові розміри. Тоді для того, щоб скласти матриці А і B потрібно до елементів матриці А додати елементи матриці B, що стоять на тих же місцях. Таким чином, сумою двох матриць А і B називається третя матриця С, яка визначається за правилом

або

Приклади.

Додавання матриць: .

Скласти 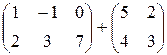не можна, оскільки розміри матриць різні.

Додавання матриць-рядків: .

Легко перевірити, що додавання матриць підкоряється наступним законам: комутативному A+B=B+A і асоціативному (A+B)+C=A+(B+C).

Помноження матриці на число. Для того, щоб помножити матрицю А на число k потрібно кожен елемент матриці А помножити на це число. Таким чином, добуток матриці А на число k є нова матриця, яка визначається за правилом , або .

Для будь-яких чисел а й b та матриць А й B виконуються рівності:

1) (ab)А=a(bА);

2) a(А+В)= aА+aВ;

3) (a+b)А=aА+bА.

Дата добавления: 2015-07-12