Робота з матрицями

Нехай потрібно задати вектор з трьох елементів, тоді їх значення треба вводити в квадратних скобках, розділяючи пробілами. Якщо необхідно задати вектор-стовпчик, то елементи вектора потрібно вводити в квадратних скобках через;

Введення матриці потребує вводу декількох рядків. Для їх розмежування використовується крапка з комою;

Часто доводиться виконувати форматування впорядкованих числових послідовностей. Такі послідовності потрібні для створення векторів або значень аргументів при побудові графіків. Для цього використовується двокрапка

х=Початкове_значення:Крок:Кінцеве_значення

Якщо крок не задано, то він по замовчуванню набуває значення 1:

Можна почати набирати в командному рядочку

Потім натиснути “Enter”

Продовжуємо вводити матрицю по рядках, останній рядок завершити квадратною скобкою:

Ще матрицю можна ввести таким чином, як ряд векторів стовпчиків:

Переглянути змінні робочого середовища можна, набравши в командному рядочку whos:

Досить часто в лінійній алгебрі використовуються одиничні матриці (елементи головної діагоналі яких дорівнюють одиниці, а решта – нулі), нульові матриці, список таких матриць:

Формат виклику	Значення, що повертається
Eye(n)	Одинична матриця розмірності Nxn
Eye(m,n)	Одинична матриця розмірності mxn
Zeros(n)	Нульова матриця розмірності Nxn
Zeros (m,n)	Нульова матриця розмірності mxn
Ones(n)	Матриця розмірності Nxn, заповнена одиницями
Ones (m,n)	Матриця розмірності mxn, заповнена одиницями
Magic (n)	Матриця, сума елементів якої по діагоналі, в рядочку і стовпчику – однакова

Для виділення елементів матриці використовуються індекси, що беруться в круглі скобки – , де – номер рядочка, – номер стовпчика. Відлік індексів ведеться від 1. Можна використовувати групове виділення елементів матриць за допомогою позначень, характерних для циклу – beg:step:end, де beg – початкове значення індексу, step – приріст, end– кінцеве значення індексу. Відсутність початкового значення сприймається як відлік від 1, відсутність кроку відповідає одиниці, відсутність кінцевого індексу сприймається як максимальний індекс.

Формат виразу	Пояснення
X(i,:)	і-тий рядок матриці Х
X(i1:i2,:)	Рядочки матриці Х, починаючи з і1 по і2
X(i1:h:i2,:)	Рядочки матриці Х, починаючи з і1 по і2 з кроком h
X(:,j)	j-тий стовпчик матриці Х
X(:,j1:j2)	Стовпчики матриці Х, починаючи з j1 по j2
X(:,j1:h:j2)	Стовпчики матриці Х, починаючи з j1 по j2 з кроком h
X(i1:i2,j1:j2)	Підматриця, обмежена рядками з і1 по і2 та стовпчиками з j1 по j2 з можливістю встановлення кроку для кожного виміру
Tril(X)	Верхній трикутник матриці Х, включаючи головну діагональ
Triu(X)	Нижній трикутник матриці Х, включаючи головну діагональ
Diag(X)	Вектор-стовпчик, утворений елементами головної діагоналі матриці Х

З матрицями можна робити наступні перетворення:

Формат виклику	Операція, що виконується
Rot90(X)	Матриця Х перевертається на 90 градусів за годинниковою стрілкою
Rot90(X,k)	Матриця Х повертається k разів
Flipud (X)	Стовпчики матриці Х перевертаються догори ногами
Fliplr(X)	Рядки матриці Х перевертають від кінця до початку

Звернення до елементу матриці С дасть результат:

Елементи матриці можуть входити до складу виразів:

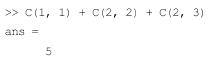
Розташування елементів матриці в пам’яті комп’ютера визначає ще один спосіб звернення до них. Матриця А розміру 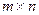зберігається у вигляді вектора довжини , в якому елементи матриці розташовані один за одним по рядочках:

Для доступу до елементів матриці можна використати один індекс, що задає порядковий номер елемента матриці в векторі. Наприклад, матриця С містися у векторі:

Індексація за допомогою порядкового номера відбувається наступним чином:

Для заміни елементу необхідно вказати ім’я елемента або матриці, його координати та присвоїти цьому імені нове значення елемента, наприклад,

Збільшити розмір матриці можна шляхом об’єднання матриць у велику. Ця процедура називається конкатенацією. Вона здійснюється шляхом утворення матриці з імен малих матриць. При цьому допускають алгебраїчні операції над іменами.

Нехай є такі вектори:

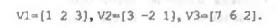
Утворюємо матрицю із цих трьох векторів. Вектори розглядаються як елементи матриці, тоді:

Виконаємо операцію конкатенації, утворимо з отриманої матриці матрицю розміром 6 на 6. Для цього утворимо нові матриці:

При використанні матричних операцій необхідно пам’ятати, що для додавання або віднімання матриці повинні бути одного розміру, а при множенні число стовпчиків першої матриці повинно дорівнювати кількості рядків другої матриці. Наприклад,

Множення матриці на число також здійснюється за допомогою зірочки, при чому множити на число можна як справа, так і зліва:

Обчислення суми елементів масиву чисел відбувається за допомогою функції – повертає значення суми елементів вектора і – повертає суми елементів і всі проміжні результати додавання.

Обчислення добутку елементів масиву здійснюється за допомогою функцій 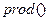– обчислює добуток елементів масиву, та – додатково повертає часткові добутки елементів вектора або стовпчиків матриці.

Нехай необхідно:

обчислити добуток чисел від 1 до 10;

добуток елементів вектора ;

добуток квадратів елементів вектора ;

часткові добутки стовпчиків матриці .

Транспонування матриці, як і вектора, відбувається за допомогою символу «.’».

Піднести квадратну матрицю до цілого ступеня можна з використанням оператора ^.

Нехай необхідно виконати такі операції з матрицями: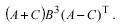

Пріоритет операцій: спочатку виконується транспонування, потім піднесення до степеню, потім множення, додавання і віднімання в останню чергу.

Так як вектор-стовпчик або вектор-рядок в Matlab представляють собою матриці, у яких один із параметрів рівний одиниці, то всі описані вище операції можна застосовувати і для множення матриці на вектор, або вектор-рядок на матрицю.

Дата добавления: 2015-07-11