Системи лінійних рівнянь

Систему лінійних рівнянь зазвичай коротко записують .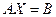

Основними характеристиками системи є:

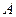- – число невідомих (число стовпчиків матриці коефіцієнтів );

- – ранг матриці коефіцієнтів ;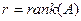

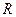- – ранг розширеної матриці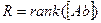

Функція 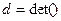обчислює визначник квадратної матриці, якщо матриця цілочисельна, приклад:

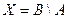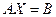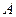Функція знаходить рішення системи рівнянь вигляду , де – прямокутна матриця розміру 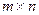і 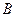– матриця розміру .

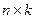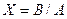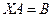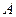Функція знаходить рішення системи рівнянь вигляду , де – прямокутна матриця розміру 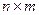і 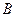– матриця розміру .

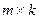Для квадратної не виродженої матриці 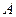, тобто її визначник не дорівнює нулю 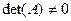, оберненою називається матриця 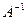, для якої

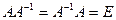, де 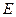– одинична матриця.

Функція 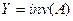обчислює матрицю, обернену квадратній матриці 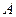. У випадках, коли матриця погано масштабована або близька до виродженої, видаються повідомлення.

Приклад:

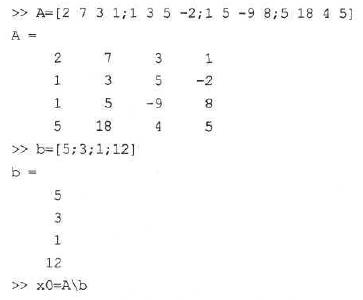
Нехай потрібно вирішити систему чотирьох лінійних рівнянь

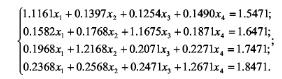
Нехай необхідно вирішити наступне рівняння: 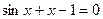. Програма вирішення цього рівняння має такий вигляд:

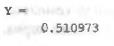
Потрібно знайти корені рівняння 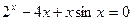, якщо відомо, що корені знаходяться поблизу значень 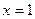та .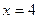

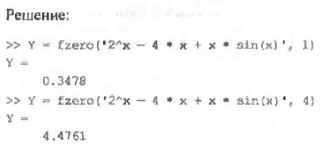
Дата добавления: 2015-07-11