Завдання до самоконтролю. Побудувати графіки наступних функцій: 1. y=4x3+15x2+12x+1; 4. y=ln(1+x2) 2. y= 5. y=1+

Побудувати графіки наступних функцій:

1.	y=4x^3+15x^2+12x+1;	4.	y=ln(1+x^2)
2.	y=	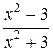5.	y=1 +
3.	y=x^2(2-х)^2;

Тема10. Диференційованість функції багатьох змінних

Нехай D(x,у) – деяка безліч точок площини Oxy. Якщо кожній впорядкованій парі чисел (x, у) з області D відповідає певне число z (zÎZ), то говорять, що z є функція двох незалежних змінних x і у. Змінні x і у називаються незалежними змінними, або аргументами, D – областю визначення, або існування, функції, а безліч Z всіх значень функції – областю її значень. Функціональну залежність z від x і у записують у вигляді z=f(x, у), z=z(x, у), z=F(x, у) і т.п.

Аналогічно визначається функція n незалежних змінних z = f(x₁, x₂,..., x_n).

Частковою похідною функції декількох змінних по одній з цих змінних називається похідна, узята по цій змінній за умови, що вся решта змінних залишається постійними. Для функції двох змінних z=f(x, у) приватною похідною по змінній x називається похідна цієї функції по x при постійному у. Позначається приватна похідна по x таким чином: .

Аналогічно частковій похідній функції z=f(x, у) по аргументу у називається похідна цій функції по у при постійному x. Позначення: .

Частковими похідними другого порядку функції z=f(x,у) називаються часткові похідні від її часткових похідних першого порядку. Якщо перша похідна була узята, наприклад, по аргументу x, то другі похідні позначаються символами

.

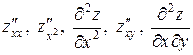Дата добавления: 2015-07-12