Приклад

Знайдіть часткові похідні другого порядку функції декількох змінних

.

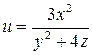Розв'язання. Для того, щоб знайти часткову похідну по х, будемо вважати, що у та z – постійні величини. Таким чином

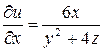. Аналогічно отримаємо:

;

.

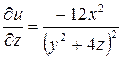Похідні другого порядку:

;

;

.

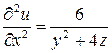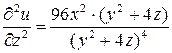Змішані похідні другого порядку:

^;

^;

.

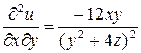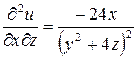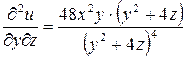Тема 11. Дослідження функції багатьох змінних на екстремум. Умовний екстремум.

Функція багатьох змінних може мати максимум або мінімум (екстремум) тільки в крапках, що лежать усередині області визначення функції, в яких всі її частинні похідні першого порядку дорівнюють нулю або не існує хоча б одна з них. Такі точки називаються критичними. Названі умови є необхідними умовами екстремуму, але ще не достатніми (вони можуть виконуватися і в точках, де немає екстремуму). Щоб критична точка була точкою екстремуму, повинні виконуватися достатні умови. Сформулюємо достатні умови екстремуму для функції двох змінних.

Теорема (достатні умови екстремуму для функції двох змінних). Нехай функція z=f(x,у): визначенав деякому околі точки M_o(x_o,у_о), в які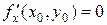й й 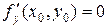; має в цій точці безперервні частинні похідні другого порядку: 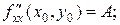. .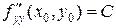Позначимо .

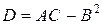Тоді:

1) якщо D > 0, то функція z має екстремум в точці M_o: максимум при А < 0, мінімум при А > 0;

2) якщо D < 0, то екстремуму в крапці M_o немає;

3) якщо D = 0, то потрібне додаткове дослідження.

Приклад: Дослідити функцію z = y⁴ - 2 xy² + x² + 2 y + y² на екстремум.

Рішення. Знаходимо частинні похідні: 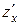= - 2 y² + 2 x,

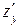= 4 y³ - 4 xy +2 +2 y.

Для відшукання критичних точок вирішимо систему рівнянь:

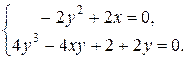
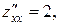
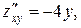
Отже, M_o(1, -1) – єдина точка, “підозріла на екстремум”. Знаходимо другі частинні похідні другого порядку: , отже, A =2, B =4, С =10, D =4, тобто D > 0, функція має екстремум в точці M_o – мінімум (A >0). Обчислимо z_min = (–1)⁴ – 2·1·(–1)² +1 – 2 +1 = –1

МОДУЛЬ 3. ІНТЕГРАЛЬНЕ ЧИСЛЕННЯ ТА ДИФЕРЕНЦІАЛЬНІ РІВНЯННЯ

Тема 12. Невизначеній інтеграл.

Функція F(x), що диференціюється в даному проміжку X, називається первісною для функції f(x), або інтегралом від f(x), якщо для всякого x 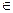X справедлива рівність:

F¢(x) = f(x)

Знаходження всіх первісних для даної функції називається її інтегруванням. Невизначеним інтегралом функції f(x) на даному проміжку Х називається безліч всіх первісних функцій для функції f(x); позначення:

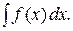
Якщо F(x) – яка-небудь первісна для функції f(x), то

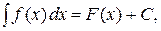
де С - довільна постійна.

Безпосередньо з визначення набуваємо основні властивості невизначеного інтеграла і список табличних інтегралів:

1) d ò f(x)=f(x)dx,

2) ò df(x)=f(x)+C,

3) ò af(x)dx=aò f(x)dx (a=const),

ò(f(x)+g(x))dx= ò f(x)dx+ ò g(x)dx.

Приклад: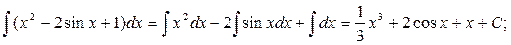

Список табличних інтегралів

1.

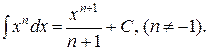
2. 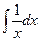= ln ê x ê+ C.

3. 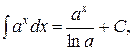(a>0, a¹1).

4. ò e^x dx = e^x + С.

5. ò sin x dx = cos x + С.

6. ò cos x dx = – sin x + С.

7. 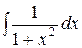= arctg x + С.

8. 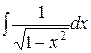= arcsin x + С.

9. 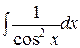= tg x + С.

10. 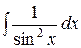= – ctg x + С.

Для інтегрування багатьох функцій застосовують метод заміни змінної, або підстановки, який дозволяє приводити інтеграли до табличної форми.

Якщо функція f(z) безперервна на [a, b], функція z=g(x) має на [а, b] безперервну похідну і a £ g(x) £ b, то

ò f (g(x)) g¢ (x) dx = ò f(z) dz,

причому після інтегрування в правій частині слід зробити підстановку z=g(x).

Для доказу достатньо записати початковий інтеграл у вигляді:

ò f(g(x)) g¢ (x) dx = ò f (g(x)) dg(x).

Приклади:

1) .

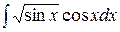Зробимо заміну t = sinx, dt = cosxdt.

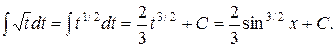
2)

Заміна 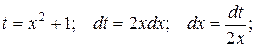Одержуємо:

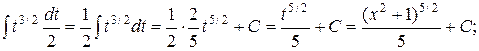
Інтегрування частинами

Нехай u=f(x) і v=g(x) – функції, що мають безперервні похідні. Тоді, за правилом диференціювання добутку,

d(uv)= udv + vdu або udv = d(uv) -vdu

Для виразу d(uv) первісною, очевидно, буде uv, тому має місце формула:

ò udv = uv – ò vdu

Ця формула виражає правило інтегрування частинами. Воноприводитьінтегрування виразу udv = uv'dx до інтегрування виразу vdu = vu'dx.

Нехай, наприклад, потрібно знайти ò x cos x dx. Покладемо u=x, dv =cos x d x, так що du=dx, v=sin x. Тоді

ò x cos x dx = ò x d (sin x)= x sin x – ò sin x dx = x sin x + cos x + С.

Приклад.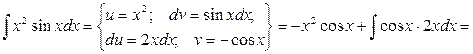

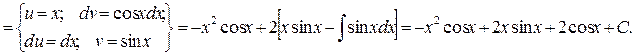Як видно, послідовне застосування формули інтегрування частинами дозволяє поступово спростити функцію і привести інтеграл до табличного.

Приклад.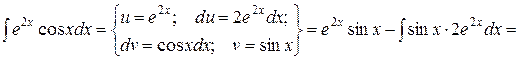

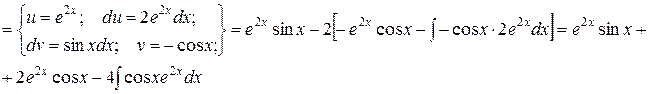
Видно, що в результаті повторного застосування інтегрування по частинах функцію не вдалося спростити до табличного вигляду. Проте, останній одержаний інтеграл нічим не відрізняється від початкового. Тому перенесемо його в ліву частину рівності.

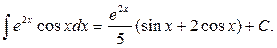
Таким чином, інтеграл знайдено взагалі без застосування таблиць інтегралів.

Інтеграл добутку синусів і косинусів різних аргументів.

a). Інтеграли від добутків синусів і косинусів з різними аргументами, лінійно залежними від х, спрощуються, якщо застосувати тригонометричні формули перетворення добутку в суму:

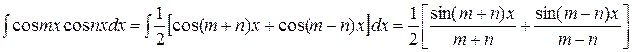
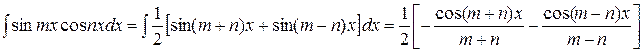
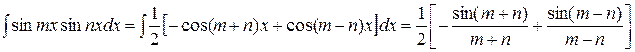
Дата добавления: 2015-07-12