Эллипс. Кривые второго порядка.

Кривые второго порядка.

Кривой 2-го порядка называется линия, которой соответствует алгебраическое уравнение 2-й степени: Ax² + Bxy + Cy² + Dx + Ey + F = 0.

Рассмотрим три вида кривых второго порядка: эллипс, гиперболу и параболу.

Эллипс.

Эллипсом называют множество точек, сумма расстояний которых от двух данных точек и 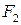– фокусов эллипса – есть величина постоянная (2a), большая расстояния между фокусами (2c).

Если центр симметрии эллипса совпадает с началом координат, а фокусы лежат на оси Ох, то уравнение эллипса имеет вид: и называется каноническим уравнением эллипса.

Термины и обозначения основных элементов эллипса:

с – фокусное расстояние; а – большая полуось эллипса; b – малая полуось эллипса.

Точки , ; , называют вершинами эллипса; точк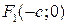и и 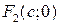– это фокусы эллипса; точка О(0; 0) называется центром эллипса.

Числа a, b, c связаны равенством: , причем .

Величина называется эксцентриситетом эллипса и характеризует степень его сжатости. Если 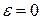, то эллипс вырождается в окружность x² + y² = R² .

Две прямые, перпендикулярные к большой оси эллипса и расположенные относительно центра на расстоянии от него, называются директрисами эллипса. Директриса называется левой, а – правой.

Если центр симметрии эллипса имеет координаты , а фокусы лежат на прямой, параллельной оси Ох, то уравнение эллипса имеет вид:

.

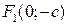Если фокусы эллипса лежат на оси Оу, а центр симметрии совпадает с началом координат, то в каноническом уравнении эллипса будет , , и , – фокусы эллипса.

Если центр симметрии эллипса находится в точке , а фокусы лежат на прямой, параллельной оси Оу, то уравнение эллипса имеет вид: .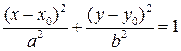

----------------------------------------------------------------------------------------------------------------

Кривые второго порядка. Стр. 1

Дата добавления: 2015-07-11