|
Читайте также: |
Гиперболой называется множество точек, модуль разности расстояний которых от двух фиксированных точек F1 и F2 (фокусов гиперболы) есть величина постоянная (2a), меньшая расстояния между фокусами (2c).
Если центр симметрии гиперболы совпадает с началом координат, а фокусы лежат на оси Ох, то уравнение гиперболы имеет вид: 
и называется каноническим уравнением гиперболы.
Термины и обозначения основных элементов гиперболы: с – фокусное расстояние; а – ве щественная полуось гиперболы; b – мнимая полуось гиперболы.
Точки 
и 
называют вершинами гиперболы, точка О(0;0) называется центром гиперболы; 
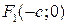и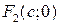 
– это фокусы гиперболы.
Числа a, b, c связаны равенством: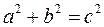 
, причем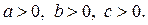 
Эксцентриситет, характеризующий степень сжатости гиперболы, равен 
, (
).
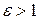Прямоугольник со сторонами 2a и 2b, расположенный симметрично относительно осей гиперболы и касающийся ее в вершинах, называется основным прямоугольником гиперболы.
Диагонали основного прямоугольника (если их неограниченно продолжать) являются асимптотами гиперболы, их уравнения: 
; 
.
Две прямые, перпендикулярные к той оси гиперболы, которая её пересекает, и расположенные симметрично относительно центра на расстоянии 
от него, называется директрисами гиперболы. Директрисы имеют уравнения: 
.
Если центр симметрии гиперболы находится в точке 
, а фокусы лежат на прямой, параллельной оси Ох, то уравнение гиперболы имеет вид:
.
Если гипербола симметрична относительно координатных осей, а ее фокусы лежат на оси Оу, то ее каноническое уравнение имеет вид: 
.
В этом случае модуль разности расстояний от любой точки гиперболы до ее фокусов равен 2b, фокусы находятся в точках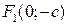 
, 
; эксцентриситет такой гиперболы определяется формулой 
, .
----------------------------------------------------------------------------------------------------------------
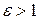Кривые второго порядка. Стр. 2
Если центр симметрии гиперболы находится в точке , а фокусы лежат на прямой, параллельной оси Оу, то ее уравнение: 
.
Если полуоси гиперболы равны, т.е. a=b, то гипербола называется равносторонней (равнобочной).
Дата добавления: 2015-07-11; просмотров: 183 | Нарушение авторских прав