Гипербола. Гиперболой называется множество точек, модуль разности расстояний которых от двух

Гиперболой называется множество точек, модуль разности расстояний которых от двух фиксированных точек F ₁ и F ₂ (фокусов гиперболы) есть величина постоянная.

Каноническое уравнение гиперболы: .

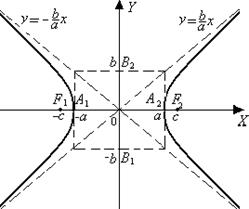· точка 0 – центр гиперболы;

· с – фокусное расстояние, F₁(-c;0), F₂(c;0);

· а – вещественная полуось гиперболы;

· b – мнимая полуось гиперболы,

· с ² = а ² + b ²;

· асимптоты

· точки A ₁и A ₂- вершины гиперболы.

· Эксцентриситет .

Сопряженная гипербола

Если фокусы гиперболы разместить на оси OY, получим уравнение сопряженной гиперболы:

.

Фокусы: F ₁(0;- c), F ₂(0; c), у которой b – вещественная

полуось, a – мнимая полуось, с ² = а ² + b ²;

асимптоты . Эксцентриситет

Дата добавления: 2015-07-11