Гипербола. Из школьного курса математики известно, что кривая, задаваемая уравнением

Из школьного курса математики известно, что кривая, задаваемая уравнением 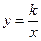, где 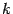-- число, называется гиперболой. Однако это -- частный случай гиперболы (равносторонняя гипербола).

Определение. Гиперболой называется геометрическое место точек плоскости, для каждой из которых абсолютная величина разности расстояний до двух фиксированных точек F ₁ и F ₂ той же плоскости, называемых фокусами гиперболы, есть величина постоянная равная 2 а.

Для получения уравнения гиперболы выберем подходящую систему координат. Начало координат расположим на середине отрезка между фокусами, ось 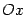направим вдоль этого отрезка, а ось ординат -- перпендикулярно к нему. По определению, абсолютная величина разности расстояний от точки гиперболы до фокусов равна .

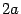Теорема. Пусть расстояние между фокусами гиперболы равно , т.е. фокусы имеют координаты F ₁(- с,0), F ₂(с,0), тогда в выбранной системе координат гипербола имеет уравнение (3), где или .

Доказательство. Пусть М (х, у) -- текущая точка гиперболы.

Так как разность двух сторон треугольника меньше третьей стороны, то 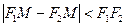, то есть 2 a < 2 c, a < c. В силу последнего неравенства вещественное число , определяемое формулой , существует.

По условию, фокусы -- F ₁(-с,0), F ₂(с,0). По формуле для случая плоскости получаем

По определению гиперболы

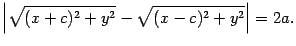
Это уравнение запишем в виде

Обе части возведем в квадрат:

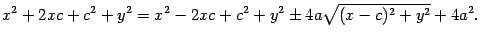
После приведения подобных членов и деления на 4, приходим к равенству

Опять обе части возведем в квадрат:

Раскрывая скобку и приводя подобные члены, получим

С учетом формулы уравнение принимает вид

Разделим обе части уравнения на и получим уравнение (3) .

Уравнение называется каноническим уравнением гиперболы. (что и треб. доказать).

Свойство. Гипербола обладает двумя взаимно перпендикулярными осями симметрии, на одной из которых лежат фокусы гиперболы, и центром симметрии. Если гипербола задана каноническим уравнением, то ее осями симметрии служат координатные оси и Оу, а начало координат -- центр симметрии гиперболы.

Определения. Точки пересечения гиперболы, заданной каноническим уравнением (3), с осью 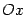называются вершинами гиперболы, отрезок между ними называется действительной осью гиперболы. Отрезок оси ординат между точками (0, - b) и (0, b) называется мнимой осью. Числа и называются соответственно действительной и мнимой полуосями гиперболы. Начало координат называется ее центром. Величина 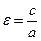называется эксцентриситетом гиперболы. Прямые , к которым график гиперболы приближается, но не пересекает, называются асимптотами гиперболы. Уравнения директрис .

Замечание. Величина с > a, то есть у гиперболы 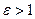. Эксцентриситет характеризует угол между асимптотами, чем ближе к 1, тем меньше этот угол.

Построение гиперболы. Чертим основной прямоугольник, т.е. прямоугольник с центром в начале координат со сторонами 2 a и 2 b, диагоналями которого будут асимптотами гиперболы.

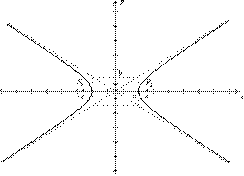
Замечание. В отличие от эллипса в каноническом уравнении гиперболы соотношение между величинами и может быть произвольным. В частности, при мы получим равностороннюю гиперболу, известную из школьного курса математики. Ее уравнение имеет знакомый вид , если взять 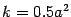, а оси и направить по биссектрисам четвертого и первого координатных углов (рис.).

Замечание 1. Если каноническое уравнение гиперболы имеет вид (3*), то ее фокусы располагаются на оси Оу, их координаты F ₁(0,- с), F ₂(0, с), числа и называются соответственно мнимой и действительной полуосями гиперболы; уравнения асимптот 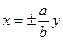, уравнения директрис .

Вообще говоря, данное уравнение (3*) не является каноническим, так как знаки перед 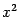и у ² противоположны знакам в первом каноническом уравнении (3). Но, если переобозначить переменные, т.е. взять 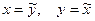, то получим снова каноническое уравнение (3): . В связи с этим уравнение (3*) будем сразу называть каноническим.

Замечание 2. Если центр гиперболы смещен и лежит в точке М ₀(х ₀, у ₀), то каноническое уравнение гиперболы примет вид: 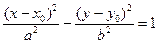(или ). Тогда координаты фокусов F ₁(х ₀- с, у ₀), F ₂(х ₀+ с, у ₀), уравнения асимптот , уравнения директрис .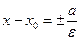

Пример 1. Постройте гиперболу , найдите ее фокусы и эксцентриситет.

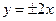Решение. Разделим обе части уравнения на 4. Получим каноническое уравнение , , . Проводим асимптоты и строим гиперболу (рис.).

Из формулы получим . Тогда фокусы -- , эксцентриситет .

Пример 2. Постройте гиперболу . Найдите ее фокусы и эксцентриситет.

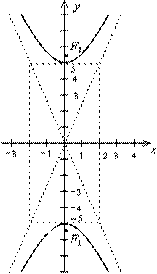Решение. Преобразуем уравнение к виду 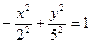. Фокусы гиперболы лежат на оси (Оу), действительная полуось b = 5, мнимая а = 2. Асимптоты имеют уравнение .

Из формулы получим , эксцентриситет , координаты фокусов .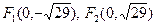

Дата добавления: 2015-07-11