Асимптоты гиперболы по каноническому уравнению. Равносторонняя гипербола. Эксцентриситет гипербол

Определение 1. Прямая называется асимптотой линии l, если точка по линии l, двигаясь к бесконечности, неограниченно приближается к данной прямой.

Теорема 1. Асимптотами гиперболы, заданной каноническим уравнением (3), являются прямые .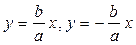

Определение 2. Эксцентриситетом e гиперболы называется число, равное отношению его фокального расстоянию с к длине его действительной полуоси a: .

Из определения гиперболы следует, что e > 1. Для окружности эксцентриситет равен нулю.

Так как , то 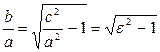. Из этого соотношения получаем, что чем ближе e к 1, тем меньше отношение b / a, и тем меньше угол между осью O x и асимптотами, чем больше e, тем больше отношение b / a, и тем больше между осью O x и асимптотами.

Определение 3. Гипербола называется равносторонней, если у нее действительная и мнимая полуоси равны, т. е. a = b.

.

5. Парабола. Каноническое уравнение параболы.

Исследование параболы по каноническому уравнению

Определение 1. Параболой называется множество всех точек плоскости, для каждой из которых расстояние до данной точки F равно расстоянию до данной прямой d, которая не проходит через точку F.

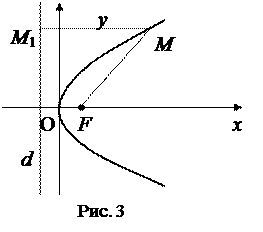Точка F называются фокусами, расстояние от фокуса параболы до директрисы называется фокальным параметром параболы и обозначается через p .

В выбранной системе координат фокус имеет координаты F (p/2, 0), директриса уравнение x = - p/2.

Пусть M (x,y)- произвольная точка плоскости O xy, M _1- проекция точки M на директрису. Точка M ₁ имеет координаты: M ₁(- p/2, y). По

определению 1 точка M принадлежит параболе тогда и только тогда, когда

| MF | = | MM ₁|. (1)

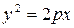. (2)

Уравнение (2) называется каноническим уравнением параболы. Отрезок | MF | называются фокальными радиусами точки M.

Исследуем параболу по каноническому уравнению.

1. Парабола проходит через начало системы координат, так как координаты точки О(0,0) удовлетворяют уравнению (2) и парабола пересекает оси только в начале координат и эта точка называется вершиной гиперболы.

2. Так как переменная y входит в уравнение (2) в четной степени, то вместе с точкой (x, y) параболе принадлежат две точки (x, ± y) (с произвольными комбинациями знаков). Таким образом, парабола симметрична относительно координатной оси O x.

3. Из уравнения параболы находим x ³ 0, и она находится в полосе 0£ x 4. Исследуем поведение параболы в первой четверти. Для этого выразим y из уравнения (2) через x:

.

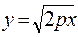Отсюда видим, что в первой четверти на промежутке 0£ x <+¥парабола является графиком возрастающей функции.

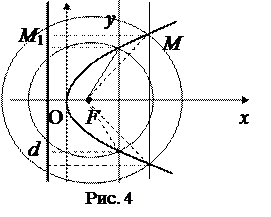4. Исследуем пересечения гиперболы с прямыми, проходящими через начало координат. Вертикальная и горизонтальная прямые, оси O х, O y пересекает параболу только в начале координат. Рассмотрим любую другую прямую, которую можно задать уравнением y = kx, k ¹ 0. Подставляя в уравнение (1) находим, что прямая пересекает параболу в двух точках .

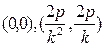Замечание 1. С помощью циркуля и линейки можно построить сколь угодно много точек на параболе. Проведем прямую параллельную директрисе на расстоянии r, и с центром в фокусе F, радиусом r. Точки пересечения прямой и окружностей лежат на параболе (см. рис. 4).

Дата добавления: 2015-07-11