Читайте также:
|
Определение 1. Эллипсом называется множество всех точек плоскости, для каждой из которых сумма расстояний до двух данных точек F 1 и F 2 той же плоскости есть величина постоянная, большая, чем расстояние между точками F 1, F 2.
Точки называются фокусами, расстояние | F 1 F 2| называется фокальным расстоянием. Обозначаем его через 2 с. Через 2 а обозначим сумму расстояний от любой точки эллипса до фокусов. По определению a > c.
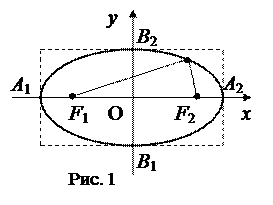Выведем уравнение эллипса в прямоугольной системе координат O xy, связанной с эллипсом. Для этого начало O системы координат поместим в середину отрезка F 1 F 2, ось O x направим по прямой F 1 F 2. Такая система координат называется канонической. В выбранной системе координат фокусы имеют координаты F 1(- c, 0) и F 2(c, 0).
Пусть M (x,y) - произвольная точка плоскости O xy. По определению 1 точка M принадлежит эллипсу тогда и только тогда, когда
| MF 1| + | MF 2| = 2 c. (1)
Находим
| MF 1| = 
, | MF 2| = 
.
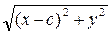Отсюда получим уравнение эллипса
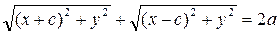. (2)
Обозначаем
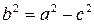
и найденное выше уравнение запишем в виде
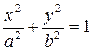. (3)
Уравнение (3) называется каноническим уравнением эллипса. Отрезки | MF 1|, | MF 2| называются фокальными радиусами точки M.
Замечание 1. Если точки F 1 и F 2 совпадают, то из определения 1 следует, что в этом случае эллипс превращается в окружность радиуса а. При этом уравнение (3) принимает вид x 2 + y 2 = a 2.
Дата добавления: 2015-07-11; просмотров: 50 | Нарушение авторских прав