Эллипс.

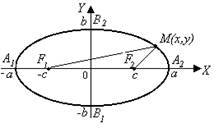
Эллипсом называют множество точек, сумма расстояний которых от двух данных точек F ₁и F ₂(фокусов эллипса) есть величина постоянная.

Каноническое уравнение эллипса: .

· точка 0 – центр эллипса;

· число с – фокусное расстояние; F₁(-c;0), F₂(c;0);

· а – большая полуось эллипса; | А ₁А₂ | = 2а

· b – малая полуось эллипса, | B₁B₂ | = 2 b

· а ² = b ² + c ²;

· точки A ₁, A ₂, B ₁ и B ₂– вершины эллипса.

Эксцентриситет – число, показывающее степень сжатия эллипса: , .

Если a= b, получится частный случай эллипса - окружность: х ² + у ² = а ².

Фокусы в этом случае совпадают с центром окружности, а - радиус.

Вертикальный эллипс

Если фокусы эллипса разместить на оси OY, то получится эллипс вертикальной формы, имеющий то же уравнение, но в котором b ² =a ²+ c ² , , F₁(0;-c), F₂(0;c).

Дата добавления: 2015-07-11