Исследование формы эллипса по его уравнению

ФЕДЕРАЛЬНОЕ АГЕНСТВО ПО ОБРАЗОВАНИЮ РФ

ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ

ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ

«ВОРОНЕЖСКИЙ ГОСУДАРСТВЕННЫЙ ПЕДАГОГИЧЕСКИЙ

УНИВЕРСИТЕТ»

КРИВЫЕ ВТОРОГО ПОРЯДКА

Учебно-методическое пособие

Для студентов I курса дневного и заочного отделений

Физико-математического факультета

Воронеж 2012

УДК 513 (075.8)

Составитель:

Кандидат физико-математических наук, доцент Н.А. Заварзина

Кривые второго порядка

Лекция №1

Эллипс

1. Определение эллипса и его уравнение

Определение. Эллипсом называется множество всех точек плоскости, для каждой из которых сумма расстояний до двух фиксированных точек плоскости F₁ и F₂ есть величина постоянная, равная 2a > ǀF₁F₂ǀ=2c.

Точки F₁ и F₂ называются фокусами эллипса, а │ F₁F₂│= 2с ─ фокальным расстоянием.

Пусть на плоскости даны две точки F₁ и F₂. Для того чтобы составить уравнение эллипса на плоскости введём ортонормированную систему координат, начало которой поместим с середину отрезка [F₁F₂]. Ось Ох расположим таким образом, чтобы точки F₁ и F₂ принадлежали этой оси.

Рис.1.

В этом случае фокусы эллипса принимают следующие координаты F₁(c;0) и F₂(-c;0). (см. Рис.1.) Пусть М(х;у) ─ произвольная точка эллипса. Тогда, по определению, │МF₁│+ │МF₂│ = 2a. (1)

По формуле вычисления расстояния между точками имеем: , . Таким образом из (1) =>

. Запишем полученное выражение в виде и возведём в квадрат. В результате, после приведения подобных членов, получаем . Для того чтобы освободиться от корня возведём последнее выражение в квадрат. В результате после элементарных преобразований имеем: . (2)

Учитывая, что > 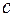обозначим (3)

и запишем (2) виде: . После деления полученного уравнения на получаем, что если точка М(х;у) принадлежит эллипсу, то её координаты удовлетворяют уравнению

(4)

Покажем теперь, что если координаты некоторой точки М₁(х₁;у₁) удовлетворяют уравнению (4), то точка М₁ принадлежит эллипсу.

Пусть для точки М₁(х₁;у₁) справедливо равенство (5)

Из (5) следует: (6)

Вычислим

=> .

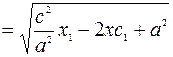
Заметим, что величина стоящая под знаком модуля положительна не только при < 0, но и при > 0 так как с < и из (6) => .

Аналогично, если провести подобные преобразования для 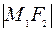, получим . => => точка М₁ принадлежит эллипсу.

Таким образом, уравнение (4) является уравнением эллипса, которое называется каноническим уравнением эллипса.

[MF₁] ─ называется первым фокальным радиусом эллипса; .

[MF₂] ─ называется вторым фокальным радиусом эллипса; .

Заметим, что если F₁= F₂, то с = 0 и 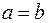=> => окружность частный случай эллипса.

Исследование формы эллипса по его уравнению

Пусть дан эллипс своим каноническим уравнением (4) .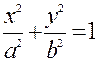

Для определения вида кривой заданной уравнением (4), заметим:

а) Координаты начала системы координат точки О(0;0) не удовлетворяют

уравнению (4). => Эллипс не проходит через начало координат.

б) Найдём точки пересечения эллипса с осью Ох: 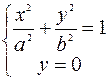=> => Эллипс две точки пересечения с осью Ох: и .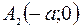

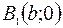в) Найдём точки пересечения эллипса с осью Оу: => => Эллипс две точки пересечения с осью Ох: и .

г) Если точка М(х;у) принадлежит эллипсу, то из уравнения (4) следует, что и точка М₁(-х;у) принадлежит эллипсу. => Эллипс симметричен относительно оси Ох.

д) Если точка М(х;у) принадлежит эллипсу, то из уравнения (4) следует, что и точка М₂(х;-у) принадлежит эллипсу. => Эллипс симметричен относительно оси Оу.

На основании г) и д) можно сделать вывод, что эллипс симметричен относительно начала системы координат.

е) Из уравнения (4) 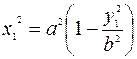, => и 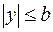=> Все точки эллипса лежат внутри прямоугольника, ограниченного прямыми и .

ж) Так как , то можно сделать вывод, что с ростом у от 0

до 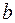величина х убывает от до 0.

з) => => =>

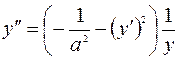<0 => Если , то 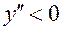, то есть функция выпукла вверх. Учитывая симметричность эллипса относительно осей координат, получаем изображение эллипса (Рис.2.).

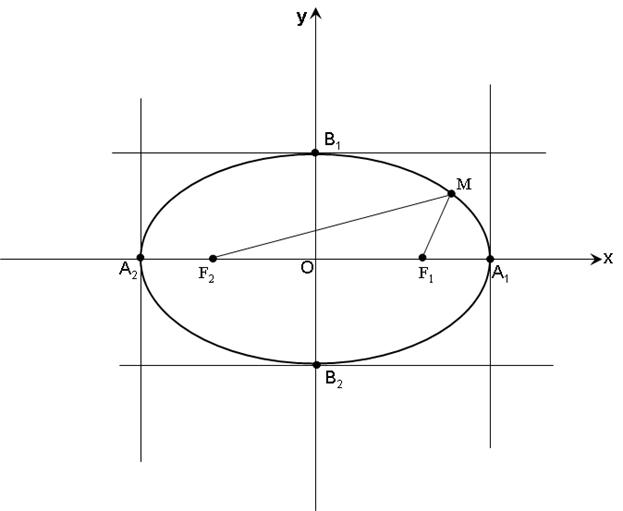
Рис.2

Точки А₁, А₂, В₁, В₂ ─ называют вершинами эллипса. [A₁A₂] ─ большой осью эллипса, [B₁B₂] ─ называют малой осью эллипса. Числа и называют полуосями эллипса.

---

Дата добавления: 2015-07-11