Параметрические уравнения эллипса

Построим на плоскости две окружности с центрами в начале координат и радиусами и 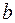. Проведём луч из начала координат, и пусть он пересечёт первую окружность в точке N₁, а вторую ─ в точке N₂. (Рис.4.)

Рис.4.

Через точку N₁ Проведём прямую ℓ₁|| (Оу), а через точку N₂ ─ прямую ℓ₂|| (Ох). Пусть М(х;у) = ℓ₁ ∩ ℓ₂. Обозначим через α = А₁ОN₁, тогда

(6)

Разделив первое равенство системы (6) на , а второе на 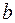, после возведения полученных равенств в квадрат и сложения их получаем:

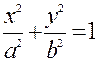=> Точка М(х;у) принадлежит эллипсу.

Соотношения (6) называют параметрическими уравнениями эллипса.

Дата добавления: 2015-07-11