Вывод уравнения геотермограммы

Вывод этого уравнения дается по проф. А.К. Козырину.

Рассмотрим решение уравнения Лапласа для случая установившегося теплообмена между двумя полупространствами, одно из которых имеет постоянную температуру. Такой процесс наблюдается, например, в породах, перекрывающих магму, при условии их горизонтального залегания и отсутствия дополнительных источников тепла (рис. 15.2).

Начало координат расположим в пределах так называемого "нейт­рального слоя", в котором сезонные и суточные колебания температуры не превышают точности измерений, а величина последней равна среднегодовой темпера­туре t0 данной местности. Оси х и у расположим в плоскости нейтрального слоя, а ось z направим вертикально вниз. Таким образом, распределение теплового поля не будет зависеть от координат х и у, следовательно, будет иметь осевую сим­метрию, а уравнение Лапласа упростится до выражения следовательно и 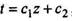где с1 и с2- постоянные, значение которых нужно определить. Поскольку , а в нашей задаче температура растет в направлении оси z, можно полагать, что с1=Г. В плоскости нейтрального слоя, при 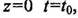, следовательно, c2=t0, и решением задачи будет выражение:

Рис. 15.2. К выводу уравнения геотермограммы

Однако это решение было бы справедливым, если бы тепловые свойства всех слоев, перекрывающих магму, были одинаковы. Но они разные. Поэтому общее решение будет иметь вид:

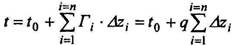где ,- мощность i-го слоя

Это уравнение линии, которая называется

ломаной геотермограммой. Уравнение одного, i-го звена геотермограммы:

откуда: Это величина маленькая, поэтому на практике оперируют с более крупной величиной которая называется геотермическим градиентом.

Среднее для всей Земли значение (15.7), хотя в разных местах значения варьируют от 0,2 до 20 . Используют также обратную величину - геотермическую ступень

(15.8)

Измерение геотермического градиента и изучение геотермограмм составляет предмет геотермии или метода естественного теплового поля Земли.

Необходимым условием получения геотермограмм в скважинах является наличие установившегося теплообмена (q = const) между скважиной и окружающими породами, т.е. равенство температур бурового раствора и горных пород.

В плоскости геологических разрезов результаты геотермических исследований изображаются в виде геотермограмм скважин t = f(H), которые представляют собой ломаные линии с точками перелома напротив границ пластов с разными тепловыми сопротивлениями (рис. 15.3). Эти графики могут быть пересчитаны в диаграммы температурного градиента или теплового сопротивления по закону Ома в дифференциальной форме, т.к. q = const, то пропорционально Гi

Строят также профили геоизотерм (рис. 15.4).

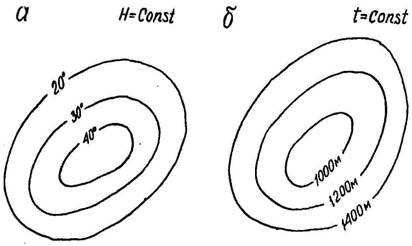
В плане результаты геотермических исследований изображают в виде планов и карт изотермических поверхностей (t=const) или карт рельефа геоизотерм (H=const), которые выглядят так, как показано на рис. 15.5, а и б.

Рис. 15.5. Карта геоизотерм (а) и карта рельефа геоизотермы t=30" (б)

Дата добавления: 2015-07-11