Физические основы метода

Согласно теории, распространение теплового поля в среде описывается дифференциальным уравнением теплопроводности (уравнение Фурье), которое для однородной изотропной среды имеет вид:

Величина, обратная λ, называется удельным тепловым сопротивлением

Интегрирование этого уравнения в условиях неустановившихся тепловых процессов, когда ∂t/∂τ≠0, представляет собой сложную задачу, решаемую лишь для наиболее простых случаев.

При установившемся процессе теплообмена ∂t/∂τ= 0 это уравнение обращается в уравнение Лапласа: V²t=0, т.е. распределение теплового поля описывается тем же законом, что и стационарное электрическое поле или гравитационное поле в пространстве, где нет дополнительных масс.

Проследим аналогию установившихся тепловых и электрических полей более подробно (табл. 15.1).

Из приведенной аналогии видно, что удельное тепловое сопротивление ξ играет такую же важную роль для тепловых полей, как и удельное электрическое сопротивление р для электрических. Значения ξ для различных горных пород приведены в табл. 15.2.

Таблица 15.2. Коэффициент теплопроводности и удельное тепловое сопротивление горных пород (по Г.А. Череменскому, 1972)

№ п/п	Горная порода, вещество	Коэффициент теплопроводности	Удельное тепловое сопротивление
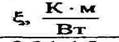
1.	Гранит	2,3-4,1	0,24-4,3
2.	Габбро	1,7-2,9	0,34-5,9
3.	Дунит	3,1-5,0	0,20-5,0
4.	Глина	0,17-1,7	0,58-5,8
5.	Песок	0,35-3,5	0,29-2,9
6.	Песчаник	0,7-5,8	0,17-1,43
7.	Известняк	0,8-4,1	0,24-1,25
8.	Каменная соль	6,2	0,16
9.	Вода	0,6	1,67
10.	Нефть	0,14	7,15
11.	Воздух	0,024	41,6

Таким образом, удельное сопротивление различных горных пород различается больше, чем на порядок. Его величина сильно зависит от пористости и влажности пород. (Последним фактором объясняется большой диапазон изменения теплового сопротивления осадочных пород).

По данным новейших исследований тепловых свойств, проведенных методом оптического сканирования (Ю. Попов и др., 2001), тепловое сопротивление горных пород очень изменчиво и в пределах интервала в 5-10 м, а иногда и участка керна длиной 7-20 см, может изменяться на 70-100%. Так же, как и электрическое сопротивление, тепловое сопротивление одних и тех же горных пород может различаться в зависимости от направления, в котором оно измеряется. Наиболее велика анизотропия тепловых свойств у слоистых горных пород. Разница в теплопроводности по слоистости и поперек нее может достигать 2,0-2,5 раз

Дата добавления: 2015-07-11