Читайте также:
|
Первая краевая задача для уравнения 
:
Найти функцию 
, определенную в области 
, 
, удовлетворяющую уравнению для 
, 
, граничным 
и начальным условиям 
Если рассматривается явление в течении малого промежутка времени, когда влияние границ ещё не существенно, то вместо полной задачи можно рассматривать предельную задачу с начальными условиями для неограниченной области:
найти решение уравнения
для 
, , с начальными условиями
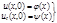при (1)
Эту задачу называют задачей Коши.
Рассмотрим задачу для неограниченной струны:
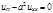(2)
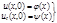(3)
Преобразуем уравнение (2) к каноническому виду
Уравнение характеристик 
, распадается на два уравнения:
, интегралами которых являются прямые
Вводя новые переменные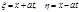 
,уравнение колебаний струны преобразуется к виду: 
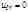(4).
Найдем общий интеграл последнего уравнения. Очевидно, для всякого решения уравнения (4) 
, где 
- некоторая функция только переменной 
. Интегрируя это равенство по при фиксированном 
, получим:
, (5) где 
и 
являются функциями только переменных и . Т.к. всякое решение уравнения (4) м.б. представлено в виде (5) при соответствующем выборе и , то формула (3) является общим интегралом этого уравнения. Сл., функция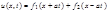 
(6) является общим интегралом уравнения (2).
Допустим, что решение рассматриваемой задачи существует, тогда оно даётся формулой (6). Определим функции и т.о., чтобы удовлетворялись начальные условия:
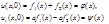
Интегрируя второе равенство получим:
,где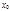 
и C – постоянные. Из равенств
находим
(7)
Т.о. мы определили функции и ч/з заданные функции 
и 
, причем равенства (7) должны иметь место для любого значения аргумента. Подставляя в (6) найденные значения и , получим:
- формула Даламбера.
Дата добавления: 2015-07-11; просмотров: 394 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Ряд Фурье с периодом . | | | В.14. Постановка краевых задач для уравнения теплопроводности. Метод разделения переменных для решения первой краевой задачи. |