Читайте также:
|
Вычисление криволинейного интеграла первого рода сводится к вычислению определённых интегралов. Пусть кривая AB задана параметрическими уравнениями 
, где 
и 
непрерывные, 
и 
- непрерывные, 
- функция, непрерывная вдоль этой кривой, причем в точке A: 
, в точке B: 
. Тогда для любой точке 
кривой AB длину 
дуги AM можно рассматривать как функцию параметра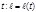 
и вычислять по формуле 
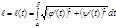откуда 
. Получаем:
2) Пусть на кривой AB определены 2 ограниченные функции 
и 
. Разобьём кривую AB на n частей точками 
. Обозначим ч/з 
и 
проекции вектора 
на оси координат, на каждой частичной дуге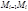 
возьмем произвольную точку 
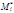и составим интегральную сумму для функции (): 
(2).
Опр. Если интегральная сумма (2) при 
- длина дуги 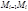имеет предел I, то этот предел называется криволинейным интегралом второгорода от функции () по кривой AB и обозначается: 
.
Сумма 
называется общим криволинейным интегралом второго рода.
Вычисление криволинейного интеграла второго рода.
Криволинейные интегралы второго рода вычисляют сведением их к определённым интегралам по формулам:
;
.
= 
(3)
Где кривая AB: ; A: , B: .
В частности, если кривая AB задана уравнением вида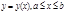 
, где y(x) – непрерывно дифференцируемая функция, то: 
, 
; 
(4)
Дата добавления: 2015-07-11; просмотров: 182 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| В.6. Криволинейный интеграл. Формула Грина. | | | В.7. Производная функции комплексного переменного. Геометрический смысл аргумента и модуля производной. Условия Коши – Римана. Аналитическая функция. |