|
Читайте также: |
Пусть функция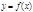 
определена на 
, 
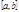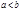. Разобьём этот отрезок на n произвольных частей точками: 
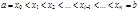. Обозначим это разбиение через 
, а точки 
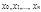называются точками разбиения. В каждом из полученных частичных отрезков 
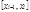выберем произвольную точку 
. 
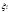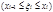Через 
обозначим разность 
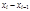, который называют длинной частичного отрезка .
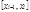Обозначим сумму:
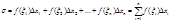,(1) которая называется интегральной суммой для функции 
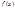на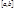 
, соответствующей данному разбиению 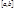на частичные отрезки и данному выбору промежуточных точек .
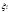Геометрический смысл суммы 
:
- это сумма площадей прямоугольников с основаниями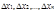 
и высотами 
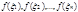если 
>0. Обозначим через 
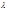- длину наибольшего частичного отрезка разбиения 
.
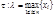Опр.: если существует конечный предел I интегрирования суммы (1) при 
, то этот предел называется определенным интегралом от функции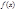 
по отрезку 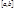, обозначается: 
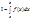или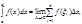 
.
Свойства:
1) 
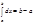2) если функция интегрируема на е, то она интегрируема на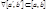 
3) если функция интегрируема на 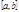и существует число 
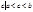, то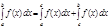 
4) если 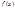и 
и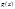нтегрируемы на 
, то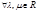 
:
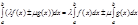
5) если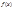 
и 
и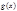нтегрируемы на 
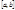, то их производные будут интегрируемы на 
.
6) если функция 
интегрируема и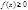 
на отрезке 
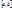, то 
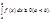7) 
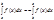
8) 
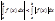
9) если 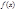и и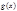нтегрируемы на , 
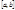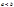и 
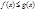, то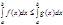 
10) если 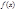интегрируема на 
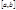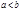, и если во всем этом промежутке имеет место неравенство 
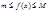, то справедливо: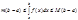 
11) Т. (о среднем): Пусть функция интегрируема 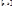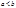на 
, 
и на 
выполняется 
, 
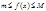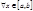тогда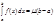 
, 
.
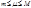Дата добавления: 2015-07-11; просмотров: 192 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Функции нескольких переменных. | | | Т. Ньютона – Лейбница. (основная формула). |