Читайте также:
|
1)Пусть дана числовая последовательность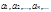 
. Выражение вида 
, называется числовым рядом или просто рядом.
Числа 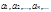называются членами ряда, член 
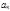с произвольным номером – общий член ряда.
Суммы конечного числа членов ряда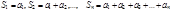 
называются частичными суммами ряда (1). Т.к. число членов ряда бесконечно, то частичные суммы ряда образуют бесконечную последовательность частичных сумм 
(2)
Ряд (1) называется сходящимися, если посл-ть его частичных сумм (2) сх-ся к какому – нибудь числу S, назыв. Суммой ряда (1):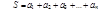 
или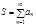 
.
Если последовательность (2) расходится, то ряд (1) – расходящийся.
Если все числа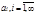 
положительны, то ряд называется знакоположительным.
Знакочередующимися называются ряды, члены которых поочередно имеют то положительный, то отрицательный знак: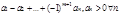 
2) Рассмотрим ряд среди членов которого имеется бесконечное множество как положительных так и отрицательных членов.
Ряд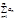 
называется абсолютно – сходящимся, если сходится ряд 
.
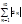Теорема. Пусть дан ряд с членами произвольных знаков. Если сходится ряд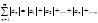 
то сходится и данный ряд.
Если ряд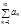 
сх-ся, но не абсолютно, то он называется условно – сходящимя.
Для ряда 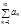обознач. 
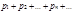(3), 
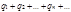(4) соот. его неотриц. и отриц. По модулю члены.
Лемма.
Если ряд 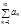условно сходится, то (3) и (4) расх-ся.
3) Теорема (признак Даламбера).
Пусть для ряда ,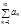 
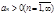существует предел 
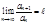; тогда при 
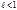ряд сходится, при 
расходится.
Дата добавления: 2015-07-11; просмотров: 232 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Т. Ньютона – Лейбница. (основная формула). | | | В.5. Функциональные ряды. Равномерная сходимость. Признак Вейерштрасса. Непрерывность суммы равномерно сходящегося ряда непрерывных функций. |