|
Читайте также: |
Ограничимся случаем функций от 3-х переменных.
Пусть в некоторой области D имеем функцию 
, возьмем точку 
в этой области. Если мы припишем 
и 
постоянные значения 
и 
и будем изменять 
, то и 
будет функцией от одной переменной в окрестности 
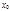. Можно поставить вопрос о вычислении её производной в точке 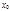. Придадим значение 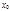приращение 
, тогда 
- частное приращение. По определению производной, она представляет собой предел
Эта производная называется частной производной функции 
по в точке 
.
Част. производ. обозначается: 
.
При условии 
функция называется дифференцируемой в точке и (только в этом случае) выражение
,
т.е линейная часть приращения функции называется её (полным) дифференциалом и обозначается 
или 
или
Д. условие диф-ти. Если функция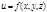 
имеет частные производные в некоторой 
окрестности точки 
и эти производные непрерывны в самой точке , то функция диф-ма в этой точке.
Н. условие диф-ти. Если функция 
диф-ма в точке 
, то она непрерывна в этой точке.
Геометрический смысл производной.
Производная функций 
в точке 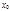геометрически представляет собой угловой коэффициент касательной, проведенной к кривой в точке .
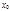Дата добавления: 2015-07-11; просмотров: 210 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| В.2. Производная и дифференциал функции одной и нескольких переменных. Необходимые и достаточные условия дифференцируемости. | | | В.3. Определённый интеграл и его свойства. Основная формула интегрального исчисления. |