include widgets/Common.h // общие функции

#include "widgets/DataSource.h" // "источник" данных

Далее идет полезный материал и образцы («мясо»).

Модель Конденсатор ()

Назначение и общие сведения. Модель Конденсатор реализована в ППП в одноименном модуле-коннекторе, и за ее «фасадом» работают модели нестационарного течения на конкретных разновидностях сопряжений двух элементов (каналов или емкостей). Все эти модели основаны на решении задачи по закону сохранения энергии в колебательном контуре, в котором имеет место подвод электрической энергии.

Если представить конденсатор в расчетной схеме замещения то для описания непосредственно через Закон сохранения энергии. Обычно принимается формула электрической энергии перетекания через конденсатор и катушку,полученная обработкой измерений с учетом этого же допущения. Вместе они составляют набор условий, связывающих параметры одномерного потока на входе с параметрами на выходе из конденсатора, и обеспечивают адекватный учет изменения параметров заряда и напряжения и в ней, вызванные как подводом (или отводом) энергии в форме электричества, так и потерями в потоке.

Модуль Конденсатор в ППП выполняет роль «мостового» коннектора между моделями двух предметных областей – «переменного тока» и «ЗСЭ». Два порта модуля на структурной схеме модели могут быть связана с компонентами первой П/О, а третий – с компонентом РОТОР второй П/О.

В качестве исходных данных в диалоговом окне описываемого модуля необходимо задать (в виде таблицы экспериментальных точек) универсальную (в обобщенных переменных) характеристику конденсатора как накопитель электрического заряда.

Математическая модель. Модели, описывающие течение рабочего заряда через конденсатор или катушку как граничные условия схемы замещения являются обобщением моделей течения на скачках cхемы. Обобщение на случай конденсатор и накопителя заряда и объемного действия состоит в применении для «замыкания» задачи более сложной статической характеристики граничного сечения в схеме замещения – универсальной характеристики конденсатор или катушки. В течении через такой элемент схемы замещения (представленный моделью связи) необходимо рассчитывать изменения и заряда, и напряжения (q*, U*), связанные с подводом или отводом энергии в форме электрической работы в необратимом квазистатическом процессе граничном сечении.

Набор соотношений может быть достаточным для более или менее адекватного выражения связи (в квазиодномерном приближении и для условий ДВС) параметров одномерного потока заряда на входе с параметрами на выходе из конденсатора, с учетом подвода к потоку или отвода от него энергии в форме электрической работы, а также необратимых потерь при течении через реальный конденсатор.

Модели течения через конденсатор, обеспечивающие корректность «сквозного» численного моделирования нестационарного течения в схеме замещения в квазиодномерной постановке, можно получить, например, прямым обобщением моделей на случай подвода или отвода работы в необратимом процессе. В принципе такое обобщение состоит лишь в применении для «замыкания» задачи о РПР универсальной характеристики более сложного вида для устройства, расположенного в граничном сечении.

Если же с одной стороны (или с обеих сторон) к модели машины в расчетной схеме замещения примыкают элемент (элементы) типа канала, то соответствующая корректная модель граничного элемента (катушки или конденсатор) должна также включать в себя условия сопряжения с моделью течения в канале. В основе модели течения в канале – система уравнений в частных производных (УЧП), описывающих квазиодномерное движения заряда. Специфические условия сопряжения следует, поэтому задавать соотношениями вдоль характеристических кривых указанной системы УЧП или соотношениями на фронтах простых изоэнтропных волн. Оба подхода к построению моделей граничных сечений дают при численном моделировании одинаковые результаты. C применением второго подхода модель для определения потоков заряда 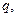энергии 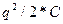в граничном сечении на шаге численного расчета можно получить обобщение на случай машины моделей местных сопротивлений соответствующего вида.

В набор условий совместности для решения задачи о РПР должна включаться универсальная расходно-напорная характеристика, позволяющая учесть действительную работу сжатия или расширения с учетом необратимых потерь в проточной части машины для текущих условий задачи о РПР на ней.

Модель Конденсатор описывает течение непосредственно через Конденсатор в допущениях об и автомодельности по числу стационарного потока на участке от входного до выходного сечения конденсатора. В силу этого привлекается универсальная характеристика компрессора, которая связывает степень повышения напряжение и внутренний КПД с обобщенными «режимными» параметрами. Этими параметрами – сопративление конденсатора и емкость конденсатора учитываются параметры в схеме замещения относительно катушки и резистора.

Прочие соотношения модели – ЗСЭ и на– необходимые условия совместности для корректного сопряжения с численным решением по уравнениям квазиодномерного нестационарного течения в канале на расчетном шаге.

Изложим модель, и метод решения уравнений модели для случая компрессора в расчетной схеме скачка сечения канала при конечных площадях сечений заметив, что прочие схемы могут рассматриваться как ее частные случаи.

Исходные данные задачи о РПР на компрессоре в выбранной схеме задаются параметрами состояния, величиной скорости одномерного потока, параметрами уравнений состояния газовых смесей в расчетных ячейках на концах примыкающих каналов и их площадями сечений, а также текущим числом оборотов в минуту рабочего колеса. В приближении совершенного газа (или смеси таких газов) задаются где

Выражение величин в уравнениях для отношения давлений , равенства давлений на КП () и непрерывности потоков массы и энергии на компрессоре (, ) через газодинамические функции стационарного и нестационарного изоэнтропного торможения и показатели компрессора и дает систему нелинейных уравнений относительно неизвестных величин – чисел 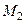, и в соответствующих зонах.

(eq_compr11_1a)

(eq_compr11_1)

(eq_compr11_1b)

где и – давления и скорости звука нестационарно заторможенного потока в зонах [compr11] из исходных данных задачи о РПР.

Метод численной реализации. Решение системы НАУ (eq_compr11_1a) – (eq_compr11_1b) можно находить итерационным методом (например, методом хорд) минимизации невязки, даваемой последним в цепочке использованных при выводе соотношений на элементах волновой картины течения при РПР (две изоэнтропные простые волны, разрывы параметров на компрессоре и на КП). Покажем применяемую нами последовательность вычислений при итерациях по неизвестной .

Решение отыскивается в области (где также и ), что возможно при когда при РПР на вход компрессора поступает смесь газов из зоны 4 ( 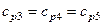). Левая граница интервала допустимых значений определяется (методом последовательных приближений) предварительно из системы условий

(eq_compr11_2)

где определяется по зависимости для левой границы области определения характеристики компрессора. Аналогично определяется и правая граница указанного интервала. Кроме того, границы интервала накладывают пределы на допустимые значения температуры стационарного торможения на входе в компрессор (при заданном числе оборотов ротора ):

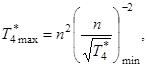
(eq_compr11_3)

С учетом условий по уравнению (eq_compr11_3) каждая из найденных ранее по уравнению (eq_compr11_2) границ интервала может быть передвинута в сторону его сужения.

На каждой итерации по текущему значению вычисляются величины статических параметров состояния в зоне 4

и параметров стационарного торможения

а также расход 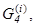по которым вычисляются определяющие параметры универсальной характеристики компрессора

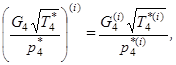
чтобы затем (с применением аппроксимации ветвей характеристик компрессора и интерполяции между ветвями) вычислить безразмерные значения его показателей в точке характеристики на текущей итерации:

На рис. fig_aproxy_compr11 показан пример аппроксимации ветвей характеристики компрессорной ступени некоторого турбокомпрессора по рядам экспериментальных точек.

Рисунок fig_aproxy_compr11 – Представление ветвей характеристики компрессора брать из PDF доки gasdyn

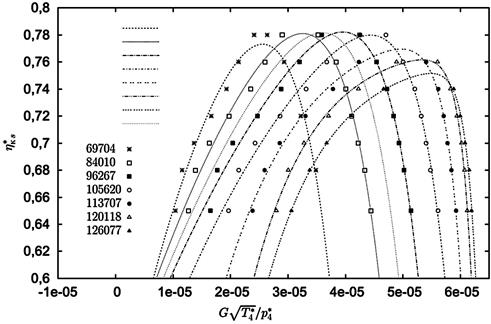
Рисунок fig_aproxy_compr11 – Представление ветвей характеристики компрессора брать из PDF доки gasdyn

Параметры потока за компрессором рассчитываются обычным для принятого допущения об адиабатности течения между сечениями 4 и 3 способом:

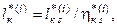
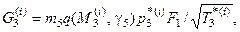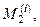Затем число определяется из уравнения после чего становятся известны статические параметры в зоне 3: давление температура скорость звука и скорость потока Далее из условия равенства давлений на КП и условия на фронте простой изоэнтропной волны определяется число а по нему – скорость в зоне 2: . Итерации по прекращаются по выполнении с заданной точностью условия равенства скоростей потока по обе стороны от КП: .

Приведенный алгоритм гарантирует отыскание решения задачи о РПР на компрессоре для точек его характеристики, входящих в области допустимых значений, заданных явным и регулярным образом. При описанном подходе достигается надежность расчета по модели для практически важных установившихся режимов работы комбинированных ДВС.

При применении в моделях элементов ГВТ нелинейных калорических уравнений состояния для рабочего тела ДВС описанная модель и процедура должны использовать корректную линеаризацию, т. к. в описанной модели и приняты постоянными.

Описанного вида модели турбин и компрессоров используются в прикладных программах, разрабатываемых на кафедре ДВС Уфимского государственного авиационного технического университета. Принятый подход к численному моделированию процессов в сложных технических системах позволяет численно рассчитывать, например, переходные процессы в ДВС со свободным турбокомпрессором, «набирая» модель последнего из моделей компрессорной и турбинной ступеней и модели инертной вращающейся массы.

В исходных данных в диалоговом окне свойств описываемой модели необходимо задать (в виде таблицы экспериментальных точек) универсальную характеристику компрессора (как машины объемного или же динамического действия) в обобщенных переменных.

sec_gasdyn_turbineМодель ТУРБИНА (Turbine)

Назначение и общие сведения. Модель ТУРБИНА реализована в ППП в модуле-коннекторе, и имеет, в общем, те же особенности, что и модель КОМПРЕССОР. Так, в частности, обе модели основаны на расчетной схеме распада газодинамического разрыва в граничном сечении тракта, в котором к потоку подводится (или, в случае модели ТУРБИНА – отводится) энергия в форме работы сжатия или расширения в потоке газообразного рабочего тела.

Обе модели аналогичным образом должны быть замкнуты эмпирически полученной характеристикой компрессионной (в случае модели ТУРБИНА – расширительной) машины.

Математическая модель. Расчет течения на стыке двух элементов ГВТ типа емкости (рис. fig_compressor) состоит в применении указанных соотношений для определения текущих величин потоков массы и энергии , где – удельная полная энтальпия.

В основе таких моделей лежит задача о РПР начальных параметров рабочего тела на граничном элементе, свойства которого в потоке задаются статической универсальной характеристикой. Применительно к каналу, показанному на рис. fig_compressor, г, система соотношений при РПР на турбине имеет вид следующей системы НАУ:

(eq_turb_1)

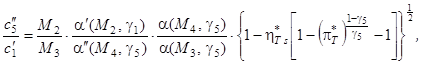(eq_turb_2)

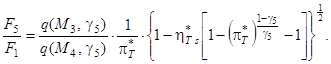(eq_turb_3)

Метод численной реализации. Способ решения задачи о РПР на турбине (ступени турбины) по соотношениям (eq_turb_1) – (eq_turb_3), т. е. для случая, показанного на (рис. fig_compressor, г). В предположениях и об автомодельности течения по и об адиабатности течения в машине (или ее ступени) характеристика может задаваться парой двухпараметрических зависимостей вида

(eq_turb10)

где для нормального направления течения , – показатели работы машины (ступени), а параметры и обобщенно учитывают режим течения для осевой и окружной компонент скорости потока. Для конкретной машины и рабочего тела (со свойствами совершенного газа) они эквивалентны соответствующим числам

Более практичным, чем по уравнению (eq_turb10) способом представления универсальной характеристики турбины является представление ее в виде наборов экспериментальных точек, для которых Для подстановки в расчетную процедуру решения задачи о РПР должны проводиться аппроксимация и дополнение ветвей характеристики. На рис. fig_aproxy_turb_10, а и б показан пример аппроксимации ветвей характеристики турбины некоторого турбокомпрессора.

Исходными данными задачи о РПР на турбине являются параметры состояния, величины скорости потока и коэффициенты уравнений состояния газовых смесей в расчетных ячейках на концах примыкающих каналов (рис. fig_compressor, г) и их площади сечений: где 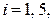а также текущее число оборотов в минуту рабочего колеса

Рисунок fig_aproxy_turb_10_1 — Представление зависимости 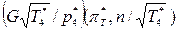брать из PDF доки gasdyn

Рисунок fig_aproxy_turb_10_2 — Представление зависимости брать из PDF доки gasdyn

Вначале по величинам статических давлений, температур и чисел в исходных данных с помощью газодинамических функций (eq_alpha1) – (eq_tau2) рассчитываются параметры нестационарного изоэнтропного торможения

Данный прием, эквивалентный временной замене турбины в граничном сечении на непроницаемую перегородку (на рис. fig_aproxy_turb_10_1 не показана), служит еще и для проверки исходных данных на предмет осуществимости течения после РПР на турбине с, 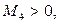т. е. в нормальном направлении (что при в принципе невозможно).

Решение задачи о РПР на турбине может отыскиваться далее любым методом минимизации невязки, полученной после применения всех алгебраических условий на элементах автомодельного решения задачи о РПР (турбина, контактный разрыв, две изоэнтропные волны. Хорошо зарекомендовал себя метод хорд для уточнения величины в диапазоне , например, правая граница которого предварительно определяется решением уравнения

в котором величина определена по характеристике из условия

Кроме того, каждая из границ диапазона может быть сдвинута (в сторону его сужения) с учетом погрешностей аппроксимации ветви по (рис. fig_aproxy_turb_10_1) и самих границ диапазона также получаемых приближенно для текущей величины частоты вращения ротора (рис. fig_aproxy_turb_10_2).

По значению на текущей итерации определяются статические параметры и параметры стационарного торможения на входе в турбину: а также расход и по ним – значение обобщенной переменной Величина степени понижения полного давления для на данной итерации определяется по характеристике турбины – из уравнения которое также может быть эффективно решено методом хорд, а внутренний изоэнтропический КПД турбины в текущем приближении – получен из

Параметры за турбиной рассчитываются обычным для принятого допущения об адиабатности течения способом:

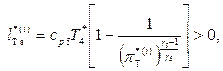
число определяется из уравнения статические параметры в зоне [turb10]: скорость звука – и потока – Далее из условий и определяется число а по нему – скорость потока в зоне [turb10]: .

Итерации по M ₄ прекращаются по выполнении равенства .

Данная последовательность расчета гарантирует нахождение решения задачи о РПР на турбине при применении модели для условий ГВТ ДВС. С небольшими изменениями она может применяться в вариантах расположения турбины на стыке канала и емкости, а также к описанию течения через компрессионную машину (ступень). При использовании моделей каналов и емкостей (где принята нелинейная температурная зависимость внутренней энергии рабочего тела) совместно с подобными моделями граничных элементов (где и приняты постоянными) должна проводиться линеаризация.

В качестве исходных данных для работы данной модели в диалоговом окне модуля должна быть задана (в виде таблицы экспериментальных точек) универсальная характеристика газовой турбины – в обобщенных переменных.

Не хватает шаблона описания реального расчетного проекта?:

(а) проект-прототип («на посмотреть»?);

(б) реальный расчетный проект (поведем проект и сделаем «реальным»).

(обсудить с НР!)

ВВЕДЕНИЕ

как образец – из «крутого» НИР

Заданием на V этап НИР предусмотрены:

1. Внедрение моделей управления в пакет.

2. Совершенствование ППП в части сервисных возможностей поддержки методик.

3. Тестовые и прикладные расчеты по детальным моделям газообмена и горения.

4. Проведение расчетных работ по методикам синтеза, включающим моделирование рабочего процесса ДВС и процессов в системах ДВС.

5. Технико-экономическая оценка полученных результатов.

6. Разработка описания методологии проектирования ДВС.

7. Разработка руководства пользователя.

8. Разработка руководства программиста.

В разделе 1 отчета описана интеграция моделей из предметной области «управление» в пакет прикладных программ (ППП).

Раздел 2 отчета посвящен совершенствованию ППП в части сервисных возможностей поддержки методик.

В разделе 3 приведены результаты тестовых и прикладных расчеты по детальным моделям газообмена и горения.

В разделе 4 приведены результаты проведенных расчетных работ по методикам синтеза, включающим моделирование рабочего процесса ДВС и процессов в системах ДВС. В расчетах по «быстросчетным» моделям нестационарного течения рабочего тела и рабочего процесса ДВС («термогазодинамика») применялись методики идентификации модели и параметрического синтеза. Для задания в быстросчетной модели характеристик элементов газовоздушного тракта проведены предварительные расчеты течений в 2D и в 3D. После идентификации модели проведена ее верификация; на обоих этапах получены оценки погрешности расчетного определения показателей ДВС.

В разделе 5 приведено концептуальное описание разработанной методологии проектирования двигателей и иных сложных технических объектов.

В разделе 6 приведена технико-экономическая оценка полученных результатов.

В приложении Е приведены материалы, подтверждающие выполнение индикаторных показателей проекта (нарастающим итогом на дату окончания 5-го этапа) и сведения о применении результатов разработки.

Руководства пользователя и программиста оформлены в виде отдельных материалов (прилагаются).

ЗАКЛЮЧЕНИЕ

как образец – из «крутого» НИР

В соответствии с заданием на отчетном этапе НИРС разработаны и интегрированы модели компрессорной (КОМПРЕССОР) и турбинной (ТУРБИНА) ступеней агруправления в пакет прикладных программ (ППП). Тестированием моделей управления в среде ППП посредством расчетных проектов с использованием реализованных моделей установлена их адекватность – показано, что результаты моделирования не противоречат ранее опубликованным данным и позволяют получать решения, соответствующие известным частным случаям.

Проведено совершенствование ППП в части сервисных средств поддержки методик. Переработаны до полного соответствия единым стандартам интерфейсы к данным моделей, и, в частности, графический интерфейс с пользователем для их визуального редактирования. Программные компоненты ППП для поддержки расчетных методик (препроцессор данных, программа оптимизации, диспетчер параллельных вычислений) усовершенствованы в ходе применения их во всех расчетных работах. Разработан программный компонент для графического представления (визуализации) численных решений средствами ППП.

Разработаны руководство программиста и Руководство пользователя. Эти документы оформлены в виде отдельных томов документации на пакет прикладных программ.

В ходе работ по моделям и программным средствам для моделирования пространственных течений рабочих тел решен ряд тестовых и прикладных задач.

Получены результаты расчетных работ по методикам синтеза систем, включающим моделирование рабочего процесса ДВС. Произведена дополнительная апробация (применительно к ДВС иного типа) методики синтеза систем ДВС, включающей моделирование рабочего процесса; расчеты велись по указанной методике с целью оценки работоспособности и текущей доводки базовых моделей, программных средств и методик моделирования; работы выполнялись на конкретных практических задачах методом численного эксперимента с применением методов параметрического синтеза. В структурной модели газовоздушного тракта двигателя на основе моделей предметной области «термогазодинамика» задавались характеристики его элементов (продувочные характеристики газообменных окон и нестационарная газодинамическая характеристика разветвления). Ввиду недостаточной точности результатов прямого моделирования по таким моделям применяется технология идентификации модели процессов с использованием данных о показателях двигателя на стенде. Программно реализована и отлажена соответствующая расчетная методика, которая в данном случае включала параметрическую идентификацию коэффициентов модели течения на органах газообмена После идентификации модели проведена ее верификация; в которой показана адекватность модели при значительном изменении профиля настроенной выпускной трубы. Реализованные и опробованные процедуры идентификации будут применяться для решения задач параметрического синтеза в целях совершенствования процессов газообмена в других двигателях.

Дано описание применяемой методологии проектирования ДВС на основе методов и средств расчетного синтеза оптимальных технических систем.

Дана технико-экономическая оценка полученных результатов. На основе сравнения показателей конкурентоспособности и технического уровня базового и разрабатываемых пакетов определен коэффициент эквивалентности разработанного пакета. Полученное значение коэффициента эквивалентности больше единицы (1,185) свидетельствует о конкурентоспособности и технической прогрессивности разработанного ППП.

СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ

как образцы

1 Баскин, В.Э. Теория несущего винта / В.Э. Баскин, Л.С. Вильгруде, Е.С. Вождаев, Г.И. Майкапар – М.: Машиностроение, 1973. – 364 с.

2 Гроп, Д. Методы идентификации систем/ Д. Гроп. – М: Мир, 1979. – 302 с.

3 Данилкин, Е.А. Параллельная реализация численного метода решения системы уравнений Навье – Стокса при моделировании крупных вихрей турбулентных течений / Е.А. Данилкин, А.В. Старченко // Т. 7, вып. 2009 г.

4 Данилкин, Е.А. К вопросу об эффективности 3D декомпозиции при численном решении уравнения переноса с использованием МВС с распределенной памятью / Вестник ТГУ. Томск: ООО «Издательство научно-технической литературы», 2008. № 2. – С. 39 – 46.

5 Дейч, А.М. Методы идентификации динамических объектов/ А.М. Дейч. – М: Энергия, 1979 – 240 с.

6 Еникеев, Р.Д. Расчетно-экспериментальное совершенствование процессов газообмена двигателя АПД – 800 / Р.Д. Еникеев, В.Ю. Иванов, В.С. Михайлов, В.Ф. Нурмухаметов, С.П. Павлинич, А.А. Черноусов // Вестник УГАТУ, Уфа: УГАТУ, 2010, т. 14, № 2 (37). – c. 13 – 20.

7 Еникеев, Р.Д. Методология моделирования процессов в рабочей камере и системах ДВС, нацеленная на решение задач параметрического анализа и синтеза двигателей. Этап 2: Разработка и совершенствование базового ряда быстросчетных моделей. Входное тестирование детальных моделей: Отчет о НИР (промежуточный) // Р.Д. Еникеев, А.А. Черноусов, И.И. Голичев, В.А. Целищев и др. – УГАТУ, Уфа, 2009 г. – 247 с.

8 Еникеев, Р.Д. Методология моделирования процессов в рабочей камере и системах ДВС, нацеленная на решение задач параметрического анализа и синтеза двигателей. Этап 3: Тестирование термогазодинамических и трибологических моделей и модификаций детальных моделей и методов их реализации: Отчет о НИР (промежуточный) // Р.Д. Еникеев, А.А. Черноусов, А.О. Борисов, Ю.Р. Вахитов и др. – УГАТУ, Уфа, 2010 г. – 328 с.

9 Еникеев, Р.Д. Методология моделирования процессов в рабочей камере и системах ДВС, нацеленная на решение задач параметрического анализа и синтеза двигателей. Этап 4: Тестирование термогазодинамических и трибологических моделей и модификаций детальных моделей и методов их реализации: Отчет о НИР (промежуточный) // Р.Д. Еникеев, А.А. Черноусов, А.О. Борисов, Ю.Р. Вахитов и др. – УГАТУ, Уфа, 2010 г. – 269 с.

10 Кудинов, П.И. Сравнительное тестирование моделей турбулентности Спаларта – Аллмараса и Ментера на задаче о трансзвуковом обтекании одиночного профиля // Днепропетровский национальный университет 14.09.2004 (автореферат).

11 Михайлов, В.С. Численное моделирование газообмена двухтактного ДВС с применением параметрической идентификации / В.С. Михайлов, А.А. Черноусов // Вестник Академии Военных Наук, Москва, 2011. – № 2 (35). – c. 239 – 244.

12 Михайлов, В.С. Методика параметрической идентификации одномерной модели газообмена двухтактных ДВС / Дисс. … канд. техн. наук. –Уфа: УГАТУ, 2011. – 159. c.

13 Попов, Е.П. Теория линейных систем автоматического регулирования / Е.П. Попов – М.: Наука, 1989. – 304 с.

14 Райков, И.Я. Испытания двигателей внутреннего сгорания /И.Я. Райков. – М.: Высшая школа, 1975. – 314 с.

15 Рудой, Б.П. Определение продувочных характеристик рабочих камер двигателей внутреннего сгорания вычислительным экспериментом / Б.П. Рудой, А.А. Черноусов // Тр. Межд. научно-техн. конф, 23-25 апреля 2003 г., г. Челябинск – Челябинск: ЮУрГУ, 2003. – с. 133 – 140.

16 Стефановский, Б.С. Испытания двигателей внутреннего сгорания/ Б.С. Стефановский и др. - М: Машиностроение, 1972 – 367 с.

17 Хусаинов, А. Ш. Теория автомобиля. Конспект лекций / А. Ш. Хусаинов, В. В. Селифонов – Ульяновск: УлГТУ, 2008. – 121 с.

18 Черноусов, А.А. О достоверности результатов моделирования движения волн конечной амплитуды в длинном неразветвленном трубопроводе с местными сопротивлениями в одномерном приближении // Вестник УГАТУ, Уфа, УГАТУ, 2009, т. 12, № 1(30). – c. 197 – 210.

19 Черноусов, А.А. Определение гидравлических характеристик местных сопротивлений в газовоздушных трактах ДВС вычислительным экспериментом. // Дисс. … канд. техн. наук. Уфа, УГАТУ, 1998. – 164 с.

20 Черноусов, А.А. Основы численного моделирования рабочих процессов тепловых двигателей: учеб. пособие / А.А. Черноусов; Уфимск. гос. авиац. техн. ун-т. – Уфа: УГАТУ, 2008. – 265 c.

21 Черноусов, А.А. Модель нестационарного течения через компрессор / Вестник Академии Военных Наук, Москва, 2011. – № 2 (35). – c. 324 – 327.

22 Черноусов, А.А. Модель нестационарного течения через турбину / Вестник Академии Военных Наук, Москва, 2010. – № 1 (30). – c. 244 – 249.

23 Черноусов, А.А. Рациональная модель течения в газовоздушном тракте ДВС в квазиодномерном приближении / Материалы Международной научно-технической конференции «Двигатель-2010». – М.: МГТУ, 2010. – c. 279 – 283.

24 Bardina, J. Improved Subgrid Scale Models for Large-Eddy Simulation / J. Bardina, J.H. Ferziger, W.C. Reynolds // Am. Inst. Astronaut., 1980. – P. 80 – 135.

25 FIRE. Users Manual Version 2009. AVL List GmbH Graz, Austria, 2010.

26 Ferziger, J.H. State of the Art in Subgrid-Scale Modeling.

27 Enikeev, R. Identification technique for quasi-1D model of gas-exchange process in a two-stroke engine / R. Enikeev, A. Chernousov, V. Mikhailov.// SAE Paper 2011-01-1145, April 2011. – 10 p.

28 Kim, J. Turbulence statistics in fully developed channel flow at the low Reynolds number / J. Kim, P. Moin, R. Moser // J. Fluid Mech., Vol. 177. – P. 133 – 166.

29 Kravchencko, A.G. Numerical Studies of Flow Over a Circular Cylinder at ReD=3900 / A.G. Kravchencko, P. Moin // Physics of Fluids. 2000. Vol.12. – P. 403 – 417.

30 Leslie, D.C. Simulation for turbulent flows. Queen Mary College, London.

31 Lyn, D. A Laser-Doppler Velocimetry Study of Ensemble Averaged Characteristics of the Turbulent Near Wake of a Square Cylinder / D. Lyn, S. Einav, W. Rodi et al. // J. Fluid Mech. 1995. Vol. 304. – P. 285 − 319.

32 Morris, P.J.M. Numerical Predictions of High Speed Jet Noise / P.J.M. Morris, Q. Wang, L.N. Long, D.P. Lockard // The Pennsylvania State University. American Institute of Aeronautics and Astronautics. – P. 1 – 13.

33 Schafer, M. Benchmark Computations of Laminar Flow Around a Cylinder / M. Schafer, S. Turek // Noteson Numerical Fluid Mechanics. 1996. – P. 856 – 869.

34 Sohankar A., Davidson L., Norberg C. Numerical Simulation of Unsteady Flow Around a Square Two-Dimensional Cylinder // In Proc. 12-th Australasian Fluid Mechanics Conference, 1995. 517-520.

35 Voice, P.R. Large-eddy simulation. Retrospect and prospect. / P.R. Voice, M.W. Collins // Department of Mechanical Engineering, the City University, London, U.K. PCH Physico-Chemical Hydrodуnamics, 1983, v.4, №.2. – P. 119 – 161.

36 Yang, J. An embedded-boundary formulation for large-eddy simulation of turbulent flows interacting with moving boundaries / J. Yang, E. Balaras // 2005.

37 Web-сайт: http://www.sci-lib.net/index.php?act=attach&type=post&id=17437.

38 Web‑сайт: http://www.cfdnode.com/topics-disp.php?topNo=01.

39 Web‑сайт: http://turbmodels.larc.nasa.gov/spalart.html.

40 Web‑сайт: http://www.dgp.toronto.edu/people/stam/reality/Research/pub.html.

41 Корпорация AVL List GmbH. – Web‑сайт: http://www.avl.com.

42 Корпорация Gamma Technologies, Inc. –

Web‑сайт:http://www.gtisoft.com.

43 Компания Ricardo. –

Web‑сайт:http://www.ricardo.com.

44 WxWidgets Library Licence. –

Web‑сайт: http://www.wxwidgets.org/about/licence3.txt.

Дата добавления: 2015-07-11