
Читайте также:
|
Пусть в области 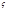 комплексной плоскости z задана функция f(z). Если для точки
комплексной плоскости z задана функция f(z). Если для точки  существует при
существует при 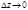 предел разностного отношения
предел разностного отношения  , то этот предел называется производной функции f(z) по комплексной переменной
, то этот предел называется производной функции f(z) по комплексной переменной  в точке
в точке  и обозначается
и обозначается  , т.е.
, т.е. 
 (1)
(1)
Функция f(z) в этом случае называется дифференцируемой в точке  .
.
Т.1. Если функция  дифференцируема в точке
дифференцируема в точке  , то в точке
, то в точке  существуют частные производные функций
существуют частные производные функций  и
и 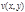 по переменным
по переменным  , причем имеют место следующие соотношения:
, причем имеют место следующие соотношения:

 (2) – условие Коши – Римана.
(2) – условие Коши – Римана.
Т.2. Если в точке  функции
функции  и
и 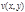 дифференцируемы, а их частные производные связаны соотношениями (2), то функция
дифференцируемы, а их частные производные связаны соотношениями (2), то функция  является дифференцируемой функцией комплексной переменной z в точке
является дифференцируемой функцией комплексной переменной z в точке  .
.
Если функция f(z) дифференцируема во всех точках некоторой области 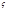 , а её производная непрерывна в этой области, то функция f(z) называется аналитической функцией в области
, а её производная непрерывна в этой области, то функция f(z) называется аналитической функцией в области 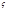 .
.
Н. и Д. условием аналитичности функции  в области
в области 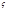 является существование в этой области непрерывных частных производных функций
является существование в этой области непрерывных частных производных функций  и
и 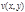 , связанные соотношениями Коши – Римана(2).
, связанные соотношениями Коши – Римана(2).
Соотношение (2) позволяют получить различные выражения для производной функции комплексной переменной

Пусть f(z) – аналитическая функция в некоторой области 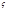 . Выберем любую точку
. Выберем любую точку  и проведем через нее произвольную кривую
и проведем через нее произвольную кривую  . Функция f(z) производит отображение области
. Функция f(z) производит отображение области 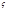 комплексной плоскости z на некот. обл.
комплексной плоскости z на некот. обл.  комплексной плоскости
комплексной плоскости  .
.
Пусть точка  переходит в точку
переходит в точку  , а кривая
, а кривая  - в проходящую через
- в проходящую через  кривую
кривую  .
.
Существует производная  функции
функции  в точке
в точке  . Пусть
. Пусть 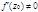 и представим
и представим  в комплексной форме:
в комплексной форме:  (3)
(3)
Выберем такой способ стремления 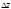 к нулю, при котором точки
к нулю, при котором точки  лежит на кривой
лежит на кривой  . Соответствующие им точки
. Соответствующие им точки  лежит на кривой
лежит на кривой  . Комплексной числа
. Комплексной числа 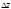 и
и  изображаются векторами секущих к кривым
изображаются векторами секущих к кривым  и
и  соответственно. Заметим, что
соответственно. Заметим, что 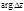 и
и  имеют геометрический смысл углов соответствующих векторов с положительными направлениями осей x и u, а
имеют геометрический смысл углов соответствующих векторов с положительными направлениями осей x и u, а  и
и  - длины этих векторов. При
- длины этих векторов. При 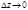 векторы секущихся переходят в векторы касательных к соответствующим кривым. Из (3):
векторы секущихся переходят в векторы касательных к соответствующим кривым. Из (3):  (4) т.е аргумент
(4) т.е аргумент  производной имеет геометрический смысл разности угла
производной имеет геометрический смысл разности угла  вектора касательной к кривой
вектора касательной к кривой  в точке
в точке  с осью u и угла
с осью u и угла  вектора касательной к кривой
вектора касательной к кривой  в точке
в точке  с осью x.
с осью x.
Т.к. производная  не зависит от способа предельного перехода, то эта разность будет той же и для любой другой кривой, проходящей через точку
не зависит от способа предельного перехода, то эта разность будет той же и для любой другой кривой, проходящей через точку  . Отсюда следует, что при отображении, осуществимом аналитической функцией
. Отсюда следует, что при отображении, осуществимом аналитической функцией  , удовлетворяющей условием
, удовлетворяющей условием 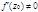 , угол
, угол  между любыми кривыми
между любыми кривыми  и
и  , пересекающимися в точке
, пересекающимися в точке  , равен углу
, равен углу  между их образами (кривыми
между их образами (кривыми 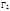 и
и  ), пересекающимися в точке
), пересекающимися в точке 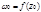 . При этом сохраняется не только абсолютная величина углов между кривыми
. При этом сохраняется не только абсолютная величина углов между кривыми  и
и  и их образами, но и направление углов. Это свойство называется свойство сохранения углов.
и их образами, но и направление углов. Это свойство называется свойство сохранения углов.
Из (3) получим  (5)
(5)
Ге6ометрический смысл этого соотношения состоит в том, что при отображении, осуществляемом аналитической функцией, удовлетворяющей условию 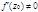 , бесконечно малые линейные элементы преобразуются подобным образом, причем
, бесконечно малые линейные элементы преобразуются подобным образом, причем  определяет коэффициент преобразования подобия. Это свойство называется свойством постоянного растяжения.
определяет коэффициент преобразования подобия. Это свойство называется свойством постоянного растяжения.
Дата добавления: 2015-07-11; просмотров: 278 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Вычисление криволинейного интеграла первого рода. | | | Опр.: Ряд вида (1) называется степенным рядом. |