Студопедия
Случайная страница | ТОМ-1 | ТОМ-2 | ТОМ-3
АрхитектураБиологияГеографияДругоеИностранные языки
ИнформатикаИсторияКультураЛитератураМатематика
МедицинаМеханикаОбразованиеОхрана трудаПедагогика
ПолитикаПравоПрограммированиеПсихологияРелигия
СоциологияСпортСтроительствоФизикаФилософия
ФинансыХимияЭкологияЭкономикаЭлектроника

Условие равномерной сходимости.

В.1.Предел и непрерывность функции одной и нескольких переменных. Свойства функций, непрерывных на отрезке. | Свойства функций непрерывных на отрезке. | В.2. Производная и дифференциал функции одной и нескольких переменных. Необходимые и достаточные условия дифференцируемости. | Функции нескольких переменных. | В.3. Определённый интеграл и его свойства. Основная формула интегрального исчисления. | Т. Ньютона – Лейбница. (основная формула). | В.4.Числовые ряды. Абсолютная и условная сходимость. Признаки сходимости: Даламбера, интегральный, Лейбница. | Вычисление криволинейного интеграла первого рода. | В.7. Производная функции комплексного переменного. Геометрический смысл аргумента и модуля производной. Условия Коши – Римана. Аналитическая функция. | Опр.: Ряд вида (1) называется степенным рядом. |


Читайте также:
  1. If <условие верно> and (a[i] < min) then
  2. Адхипати-пратьяя” – доминирующее условие.
  3. Второе условие: умение правильно задать вопрос
  4. Г) УСЛОВИЕ ПРОВЕРКИ
  5. Ключевое условие их инициации.
  6. Необходимое условие интерференции световых волн: A) когерентность
  7. Но я глубоко уверен, что первое и непременное условие в воспитании ребенка — это заботливое и бережное отношение к его личности.

Т. Больцано – Коши: Для того, чтобы посл-ть (1): 1) имела предельную функцию и 2) сходилась к этой функции равномерно относительно в X, Н. и Д., чтобы для каждого .

3) Теорема (признак Вейерштрасса)

Если числовой ряд (3) сходится и для , n=1,2,… , то ряд (2) абсолютно и равномерно сходится на X.

4) Теорема (непрерывность суммы равн. сход. ряда непрерыв. функций).

Пусть функции определены на X, все непрерывны в некоторой точке 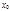. Если ряд на множестве X сходится равномерно, то и сумма ряда в точке 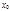также будет непрерывна.

 


Дата добавления: 2015-07-11; просмотров: 233 | Нарушение авторских прав

<== предыдущая страница | следующая страница ==>
В.5. Функциональные ряды. Равномерная сходимость. Признак Вейерштрасса. Непрерывность суммы равномерно сходящегося ряда непрерывных функций.| В.6. Криволинейный интеграл. Формула Грина.
mybiblioteka.su - 2015-2024 год. (0.006 сек.)