
Читайте также:
|
1) Пусть дана последовательность, элементами которой являются функции 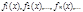 (1) и определены в некоторой области
(1) и определены в некоторой области 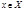 . Такая последовательность называется функциональной.
. Такая последовательность называется функциональной.
Последовательность (1) называется ограниченной на X, если для любого n,  .
.
Последовательность (1) называется сходящейся на X, если для любого фиксированного 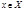 последовательность
последовательность 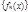 сходится (как числовая последовательность).
сходится (как числовая последовательность).
Если посл. (1) сходится на X, то функция  определенная для любых значений
определенная для любых значений 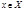 равенством
равенством  называется пределом последовательности.
называется пределом последовательности.
Рассмотрим ряд, членами которого являются функции от одной и той же переменной  в некоторой области
в некоторой области 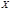 :
:  (2)
(2)
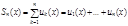 - называется частичной суммой n-го порядка,
- называется частичной суммой n-го порядка, 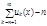 - ый остаток.
- ый остаток.
Ряд (2) называется сходящимся на X, если последовательность  его частные сумм сх-ся на этом множ-ве. При этом предел частичных сумм наз-ся суммой ряда
его частные сумм сх-ся на этом множ-ве. При этом предел частичных сумм наз-ся суммой ряда  и пишут
и пишут  , и говорят, что функция
, и говорят, что функция 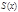 раскладывается в ряд (2).
раскладывается в ряд (2).
Множ-во всех значений  , при которых ряд (2) сх-ся, наз-ся областью сходимости ряда.
, при которых ряд (2) сх-ся, наз-ся областью сходимости ряда.
2)Пусть 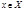 . Рассмотрим посл-ть
. Рассмотрим посл-ть  .
.

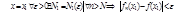
Если бы точек  было бы конечное число, то из всех N можно бало бы выбрать максимальное, для кот. для
было бы конечное число, то из всех N можно бало бы выбрать максимальное, для кот. для  выполнялось бы
выполнялось бы 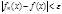 (*)
(*)
Но как правило  принадлежит множеству у которых точек бесконечно много, поэтому нер-во (*) может и не выполняться для всех
принадлежит множеству у которых точек бесконечно много, поэтому нер-во (*) может и не выполняться для всех  , начиная с одного и того же, но сущ-ние посл-ти функций, сходящейся в промежутке обладает особенностью такой, что для них N можно выбрать в зависимости от
, начиная с одного и того же, но сущ-ние посл-ти функций, сходящейся в промежутке обладает особенностью такой, что для них N можно выбрать в зависимости от  и так, что N не зависит от
и так, что N не зависит от  и выполняется неравенство (*).
и выполняется неравенство (*).
Опр.: Функциональная последовательность 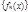 называется равномерно сходящейся на X, если для
называется равномерно сходящейся на X, если для  .
.
Опр.: Если частичная сумма  стремится к сумме ряда
стремится к сумме ряда 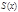 равномерно относительно
равномерно относительно  в области X, то говорят, что ряд (2) равномерно сходится в этой области.
в области X, то говорят, что ряд (2) равномерно сходится в этой области.
ИЛИ Ряд (2), сходящийся для всех  из области X, называется равномерно сходящейся в этой области, если для каждого числа
из области X, называется равномерно сходящейся в этой области, если для каждого числа 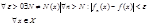 .
.
Дата добавления: 2015-07-11; просмотров: 207 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| В.4.Числовые ряды. Абсолютная и условная сходимость. Признаки сходимости: Даламбера, интегральный, Лейбница. | | | Условие равномерной сходимости. |