Читайте также:
|
1) Т. Больцано – Коши. Пусть на отрезке 
задана непрерывная функция 
. Причем на концах отрезка она имеет значения разных знаков. Тогда на 
существует по крайней мере одна точка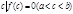 
.
2) 2-я Т. Больцано – Коши. Пусть на 
определена непрерывная функция , принимающая на концах отрезка различные значения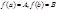 
тогда какое бы число C находящееся между A и B мы ни взяли, на 
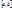найдется такое число c, что 
.
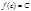3) Т. Вейерштрасса. Если функция непрерывна на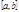 
, то она ограничена на 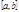, т.е. существует 
и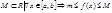 
.
4) 2-я Т. Вейерштрасса. Пусть функция непрерывна на 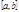. Тогда среди всех значений есть наибольшее и наименьшее значение.
Замечательные пределы: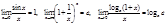 
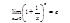
Дата добавления: 2015-07-11; просмотров: 148 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| В.1.Предел и непрерывность функции одной и нескольких переменных. Свойства функций, непрерывных на отрезке. | | | В.2. Производная и дифференциал функции одной и нескольких переменных. Необходимые и достаточные условия дифференцируемости. |