Читайте также:
|
1) Рассмотрим на плоскости 
некоторую кривую AB, гладкую или кусочно – гладкую.[Кривая, заданная уравнениями 
, называется гладкой, если функции 
и 
непрерывные производные 
и 
, не обращающиеся в ноль одновременно. Непрерывная кривая, составленная из конечного числа гладких кусков, называется кусочно - гладкой ], и предположим, что функция 
определена и ограничена на кривой AB.
Разобьем кривую AB произвольно на n частей точками 
, выберем на каждой из частичных дуг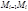 
произвольную точку 
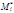и составим сумму 
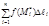(1), 
- длина дуги 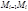. Сумма (1) называется интегральной суммой для функции 
по кривой AB. Обозначим ч/з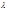 
наибольшую из длин частичных дуг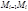 
.
Опр. Если интегральная сумма (1) при 
имеет предел, равный I, то этот предел называется криволинейным интегралом первого рода от функции 
по кривой AB и обозначается одним из следующих символов 
. В этом случае функция называется интегрируемой вдоль кривой AB, сама кривая AB – контуром интегрирования, A – начальной, а B – конечной точками интегрирования.
Дата добавления: 2015-07-11; просмотров: 175 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Условие равномерной сходимости. | | | Вычисление криволинейного интеграла первого рода. |