Опр.: Ряд вида (1) называется степенным рядом.

Т.(Абеля). Если степенной ряд (1) сх-ся при 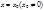, то он сх-ся, и притом абсолютно, для всех 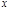, удовлетворяющих условию ; если ряд (1) расходится для всех , удовлетворяющих условию .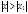

Т. Если ряд 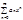сходится при всех значениях и не только при x=0, то существует число R>0, такое что ряд абсолютно сх-ся при 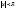и рас-ся при .

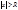Интервал (-R,R) называется интервалом сходимости степенного ряда. Число R называется радиусом сходимости.

Для ряда 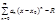- радиус сходимости, 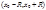- область сходимости.

Т. Если предел 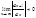, то радиус сходимости ряда 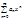равен

Т. (интегрирование и дифференцирование степенных рядов)

Если функцию 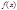можно разложить в окрестности точки 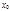в степенной ряд 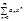с радиусом сходимости R>0, то:

1) Функция 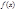имеет на промежутке (-R,R) производные от всех порядков, которые м.б. найдены из (1) почленным дифференцированием 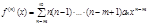(2);

2) Для 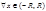справедливо тождество: 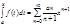(3);

3) ряды (1),(2),(3) имеют одинаковые радиусы сходимости.

Т. (выражение коэффициентов в степенные ряды ч/з его сумму)

Если функция 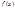раскладывается в некоторый окрестности 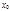в степенной ряд 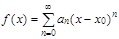, то

.

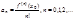Т. Если функция 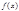на интервале (-R,R) разлагается в степенной ряд , то это разложение единственно.

Ряд вида называется рядом Маклорена функции .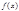

Разложение в ряд Маклорена некоторых элементарных функций.

.

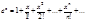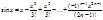
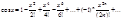
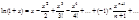
Ряд вида (4), где z – комплексная переменная; 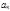и - комплексные числа, называется степенным рядом.

Т. 1) Если степенной ряд 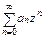(5) сходится при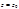 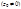, то он сх-ся и притом абсолютно, для всех z, удовлетворяющих условию 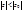; 2) если ряд (5) расх-ся при 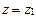, то он расх-ся для всех z, удовл. условию .

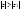Т. Если ряд (5) сх-ся не при всех значениях z и не только при z=0, то существует число R>0 такое, что ряд сходится абсолютно при 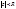и расходится при

Дата добавления: 2015-07-11