Читайте также:
|
Опр.: Пусть дана посл-ть, элементами кот-й явл-ся ф-ции 
(1) и определены в некоторой области 
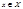. Такая посл-ть называется функциональной.
Опр.: Функциональный ряд вида 
(2) наз-ся тригонометрическим рядом.
Каждый член тригонометрического ряда – это ф-ция с периодом 
. Поэтому, если ряд (2) будет сходится, то его сумма будет периодическая с периодом 
.
Опр. Система функций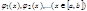 
называется ортогональной ситемой на 
, если выполняются 2 условия:
1) 
2) 
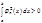
Т. Система функций 
является ортогональной системой на промежутке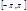 
.
Любой бесконечно дифференцируемой функции соответствует ряд Тейлора.
Возьмём функцию 
, определённую на 
и сотавим с её помощью числа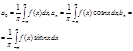 
(3)
Опр. Тригонометрический ряд, коэффициентами кот. служат числа (3) наз-ся рядом Фурье функции 
, а сами коэффициенты наз-ся коэф-ми Фурье функции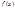 
.
Чтобы можно было вычислить коэф-ты Фурье, нужно предположить, чтобы функция 
была интегрируема на 
, след. каждой такой функции можно поставить в соответствие ряд Фурье. е
Утв. Если функциональный ряд 
сх-ся на 
и 
некоторая ограниченная на 
функция, то ряд 
также будет равномерно сходится на .
Т. Если функция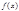 
разлагается на 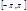в равномерно сходящийся тригонометрический ряд есть её ряд Фурье.
Дата добавления: 2015-07-11; просмотров: 233 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Опр.: Ряд вида (1) называется степенным рядом. | | | Сходимость ряда Фурье. |