Сходимость ряда Фурье.

Функции нескольких переменных. | В.3. Определённый интеграл и его свойства. Основная формула интегрального исчисления. | Т. Ньютона – Лейбница. (основная формула). | В.4.Числовые ряды. Абсолютная и условная сходимость. Признаки сходимости: Даламбера, интегральный, Лейбница. | В.5. Функциональные ряды. Равномерная сходимость. Признак Вейерштрасса. Непрерывность суммы равномерно сходящегося ряда непрерывных функций. | Условие равномерной сходимости. | В.6. Криволинейный интеграл. Формула Грина. | Вычисление криволинейного интеграла первого рода. | В.7. Производная функции комплексного переменного. Геометрический смысл аргумента и модуля производной. Условия Коши – Римана. Аналитическая функция. | Опр.: Ряд вида (1) называется степенным рядом. |

Читайте также:

Будем говорить, что функция 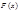, определённая на всей числовой прямой и периодическая с периодом 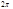, является периодическим продолжением функции 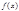; если н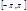а . Если на 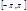ряд Фурье сх-ся к функции 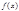, то он сх-ся на всей числовой прямой к её периодическому продолжению.

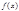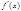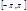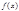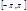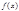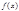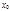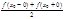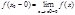Т. Пусть функция и её производная - непрерывные функции на или же имеют на нём конечное число точек разрыва 1-го рода. Тогда ряд Фурье функции сх-ся на всей числовой прямой, причем в каждой точке , в которой непрерывна, сумма ряда равна , а в каждой точке разрыва функции сумма ряда равна , где и 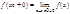. На концах отрезка 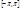сумма равна . В любой точке 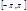сумма ряда Фурье равна , если x – точка непрерывности 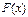, и равна , если x – точка разрыва 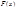, где 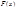- периодическое продолжение функции .

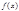Дата добавления: 2015-07-11; просмотров: 189 | Нарушение авторских прав

<== предыдущая страница	\|	следующая страница ==>
В.9. Ряд Фурье по ортогональной системе функций. Неравенство Бесселя, равенство Парсеваля, сходимость ряда Фурье.	\|	Ряд Фурье с периодом .

mybiblioteka.su - 2015-2024 год. (0.007 сек.)