Сходимость метода.

В общем случае сходимость итерационной последовательности зависит от и начального приближения . Она может сходиться и иметь предел или расходиться (не имея предела). Если предел 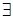-ет:

То он является решением нашей функции, а метод называется сходящимся. Опыт показывает, что возможен случай, когда метод сходится и расходится. С мат. точки зрения эта ситуация сходна с сжимающими отображениями. Если отображение сжимающее, то последовательность сходящаяся. Если условие сжимаемости не выполнено, то возможны два варианта:

1. через некоторое время элемент последовательности попадёт в зону сжимающегося отображения, и последовательность будет сходиться, но уже к другому корню.

2. последовательность уйдёт на бесконечность. В этом случае она ни когда не сойдется.

Если задана функция 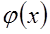, то у корней может находиться некая область, где отображение сжимается, - это область сходимости. Если корень попал в такую область сходимости, то выбрав в качестве начального приближения любую точку этой области мы получим в пределе корень. Если выбрать вне этой области - не найдём. Если вокруг корня нет области, то получить его нельзя.

Функцию надо подбирать так чтобы вокруг нужного нам корня была область сходимости.

В итерационном методе хорд пользуются формулой

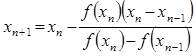
Чебышев предложил рассматривать не функцию f, а функцию обратную к ней:

+..

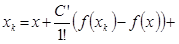
Для k+1 –го элемента формула метода Чебышева:

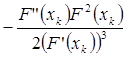
Если x – начальное приближение к корню, то элементы данного ряда дают последовательное приближение:

1- е приближение: и т.д. В рекуррентной форме получаем формулу Ньютона:

Формула Ньютона соответствует методу касательных Ньютона. Фактически, производная функции определяет наклон касательной, т.е. в каждой точке мы берём касательную к заданной функции – метод касательных – предельный случай метода хорд.

Дата добавления: 2015-07-11