Полином Лагранжа

Лагранж предложил строить интерполяционный полином в следующем ви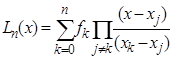де:

, где - узлы интерполяции, - исследуемая точка, - значение интерполируемой функции в узле i. Условие интерполяции для полинома Лагранжа . Полином Лагранжа удовлетворяет условию интерполяции.

Полином Лагранжа по сравнению с каноническим полиномом имеет важное преимущество – он вычисляется прямым способом, без решения системы уравнений. Это значительно облегчает вычисления. Кроме того, существует специальная вычислительная схема Эйткена, которая позволяет вычислять значения полинома Лагранжа быстрым способом (похожим на схему Горнера):

L_012…n(x) = [(x-x₀)*L_12…n(x) - (x-x_n)*L_012…n-1(x)]/[x_n –x₀]

Здесь L_012…n – полином n порядка по всем узлам, L_12…n - полином n-1 порядка по узлам от 1 до n-го, L_012…n-1 - полином n-1 порядка по узлам от 0 до n-1. Таким образом, схема расчета ведется по увеличению степени полинома. Минимальная степень n=0, тогда полином просто равен значению функции.

Замечание. Следует учитывать, что интерполяционный полином N-го порядка, заданный на N-1 узле интерполяции единственный. Поэтому вычисления полинома Лагранжа или полинома Ньютона дают одинаковый результат. Но форма полиномов и расчет их отличается, поэтому отличается погрешность и скорость вычисления. Вычисление по схеме Эйткена не выделяют вид полинома, поэтому эта схема вычисляет некий абстрактный интерполяционный полином.

Дата добавления: 2015-07-11