Вариационные задачи на условный экстремум. Метод множителей Лагранжа.

Пусть в пространстве C¹[a,b] заданы функционалы

Ставится задача исследовать функционал Ф(x) на экстремум на множестве

G={x(t)Є C¹[a,b] | x(a)=A, x(b)=B, Ψ_i(x)=α_i, α_i=const}

Система решения поставленной задачи методом множителей Лагранжа:

1. Составим функцию Лагранжа

2. Выписываем уравнение Эйлера

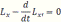
3. Находим допустимые экстремали (решения уравнения Эйлера). Константы и значения λ_i определяем из условий

4. По определения min, max функционала исследуем знак разности

Где x₀ – допустимая экстремаль

Если , то

Если , то

2. 2.

При условиях , 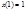и связи исследовать на экстремум функционал .

1. Составим функцию Лагранжа

2. Выпишем уравнение Эйлера

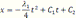
3.

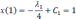
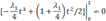
Получаем - допустимая экстремаль

4. Пусть h=x-x₀

Так как h(0)=h(1)=0 то разность

Таким образом на G

Дата добавления: 2015-07-12